|
|
|
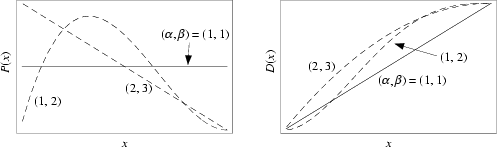
A general type of statistical Distribution which is related to the Gamma Distribution. Beta distributions have
two free parameters, which are labeled according to one of two notational conventions. The usual definition calls these
![]() and
and ![]() , and the other uses
, and the other uses
![]() and
and
![]() (Beyer 1987, p. 534). The
above plots are for
(Beyer 1987, p. 534). The
above plots are for
![]() [solid], (1, 2) [dotted], and (2, 3) [dashed]. The probability function
[solid], (1, 2) [dotted], and (2, 3) [dashed]. The probability function ![]() and Distribution Function
and Distribution Function ![]() are given by
are given by
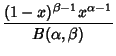 |
|||
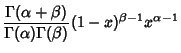 |
(1) | ||
| (2) |
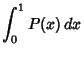 |
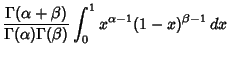 |
(3) | |
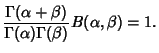 |
(4) |
| (5) |
| (6) |
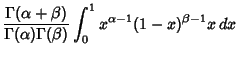 |
|||
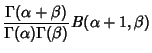 |
|||
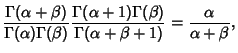 |
(7) |
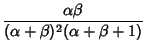 |
(8) | ||
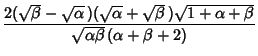 |
(9) | ||
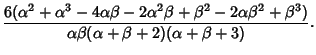 |
|||
| (10) |
| (11) |
In ``normal'' form, the distribution is written
| (12) |
| (13) | |||
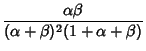 |
(14) | ||
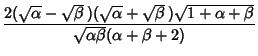 |
(15) | ||
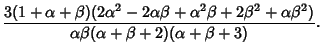 |
|||
| (16) |
See also Gamma Distribution
References
Abramowitz, M. and Stegun, C. A. (Eds.).
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, pp. 944-945, 1972.
Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, pp. 534-535, 1987.
|
|
|
© 1996-9 Eric W. Weisstein