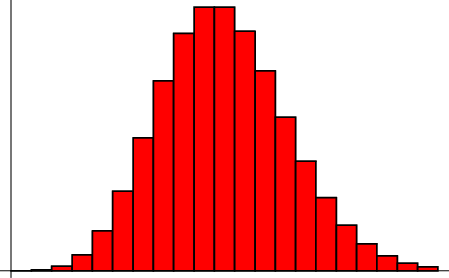
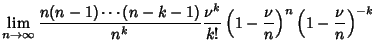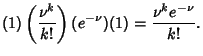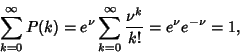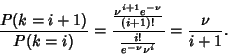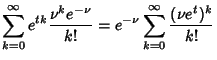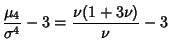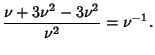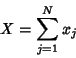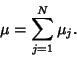A Poisson distribution is a distribution with the following properties:
- 1. The number of changes in nonoverlapping intervals are independent for all intervals.
- 2. The probability of exactly one change in a sufficiently small interval
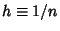 is
is
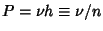 ,
where
,
where 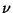 is the probability of one change and
is the probability of one change and 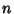 is the number of Trials.
is the number of Trials.
- 3. The probability of two or more changes in a sufficiently small interval
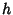 is essentially 0.
is essentially 0.
The probability of 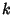 changes in a given interval is then given by the limit
of the Binomial Distribution
changes in a given interval is then given by the limit
of the Binomial Distribution
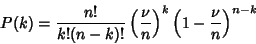 |
(1) |
as the number of trials becomes very large,
This should be normalized so that the sum of probabilities equals 1. Indeed,
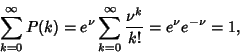 |
(3) |
as required. The ratio of probabilities is given by
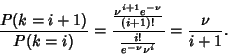 |
(4) |
The Moment-Generating Function of this distribution is
so
The Moments about zero can also be computed directly
as can the Moments about the Mean.
so the Mean, Variance, Skewness, and Kurtosis are
The Characteristic Function is
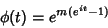 |
(24) |
and the Cumulant-Generating Function is
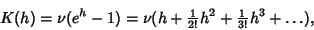 |
(25) |
so
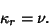 |
(26) |
The Poisson distribution can also be expressed in terms of
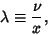 |
(27) |
the rate of changes, so that
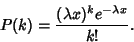 |
(28) |
The Moment-Generating Function of a Poisson distribution in two variables is given by
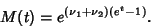 |
(29) |
If the independent variables 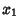 ,
, 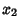 , ...,
, ..., 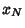 have Poisson distributions with parameters
have Poisson distributions with parameters 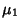 ,
, 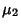 ,
...,
,
..., 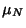 , then
, then
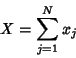 |
(30) |
has a Poisson distribution with parameter
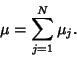 |
(31) |
This can be seen since the Cumulant-Generating Function is
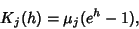 |
(32) |
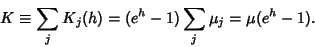 |
(33) |
References
Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 532,
1987.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T.
``Incomplete Gamma Function, Error Function, Chi-Square Probability Function, Cumulative Poisson Function.'' §6.2 in
Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge
University Press, pp. 209-214, 1992.
Spiegel, M. R. Theory and Problems of Probability and Statistics. New York: McGraw-Hill, p. 111-112, 1992.
© 1996-9 Eric W. Weisstein
1999-05-25