A surface of revolution is a Surface generated by rotating a 2-D Curve about an axis. The resulting surface
therefore always has azimuthal symmetry. Examples of surfaces of revolution include the Apple, Cone (excluding
the base), Conical Frustum (excluding the ends), Cylinder (excluding the ends), Darwin-de Sitter Spheroid,
Gabriel's Horn, Hyperboloid, Lemon, Oblate Spheroid, Paraboloid, Prolate Spheroid,
Pseudosphere, Sphere, Spheroid, and Torus (and its generalization, the Toroid).
The standard parameterization of a surface of revolution is given by
For a curve so parameterized, the first Fundamental Form has
Wherever 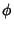 and
and
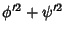 are nonzero, then the surface is regular and the second
Fundamental Form has
are nonzero, then the surface is regular and the second
Fundamental Form has
Furthermore, the unit Normal Vector is
![\begin{displaymath}
\hat {\bf N}(u,v)={\mathop{\rm sgn}\nolimits (\phi)\over\sqr...
...left[{\matrix{\phi'\cos u\cr \psi'\sin u\cr \phi'\cr}}\right],
\end{displaymath}](s3_1672.gif) |
(10) |
and the Principal Curvatures are
The Gaussian and Mean Curvatures are
(Gray 1993).
Pappus's Centroid Theorem gives the Volume of a solid of rotation as the cross-sectional Area times
the distance traveled by the centroid as it is rotated.
Calculus of Variations can be used to find the curve from a point 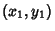 to a point
to a point 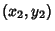 which, when
revolved around the x-Axis, yields a surface of smallest Surface Area
which, when
revolved around the x-Axis, yields a surface of smallest Surface Area 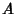 (i.e., the Minimal Surface).
This is equivalent to finding the Minimal Surface passing through two circular wire frames. The Area element is
(i.e., the Minimal Surface).
This is equivalent to finding the Minimal Surface passing through two circular wire frames. The Area element is
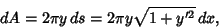 |
(15) |
so the Surface Area is
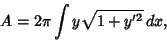 |
(16) |
and the quantity we are minimizing is
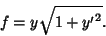 |
(17) |
This equation has 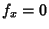 , so we can use the Beltrami Identity
, so we can use the Beltrami Identity
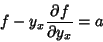 |
(18) |
to obtain
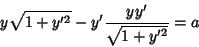 |
(19) |
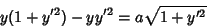 |
(20) |
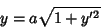 |
(21) |
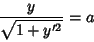 |
(22) |
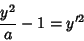 |
(23) |
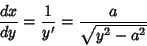 |
(24) |
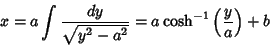 |
(25) |
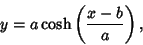 |
(26) |
which is called a Catenary, and the surface generated by rotating it is called a Catenoid. The two constants
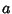 and
and 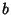 are determined from the two implicit equations
are determined from the two implicit equations
which cannot be solved analytically.
The general case is somewhat more complicated than this solution suggests. To see this, consider the Minimal Surface
between two rings of equal Radius 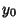 . Without loss of generality, take the origin at the midpoint of the two rings.
Then the two endpoints are located at
. Without loss of generality, take the origin at the midpoint of the two rings.
Then the two endpoints are located at 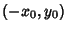 and
and 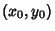 , and
, and
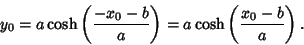 |
(29) |
But
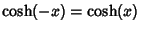 , so
, so
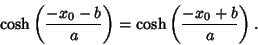 |
(30) |
Inverting each side
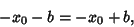 |
(31) |
so 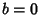 (as it must by symmetry, since we have chosen the origin between the two rings), and the equation of the
Minimal Surface reduces to
(as it must by symmetry, since we have chosen the origin between the two rings), and the equation of the
Minimal Surface reduces to
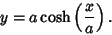 |
(32) |
At the endpoints
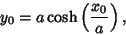 |
(33) |
but for certain values of 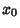 and
and 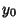 , this equation has no solutions. The physical interpretation of this fact is that
the surface breaks and forms circular disks in each ring to minimize Area. Calculus of Variations cannot be used
to find such discontinuous solutions (known in this case as Goldschmidt Solutions). The
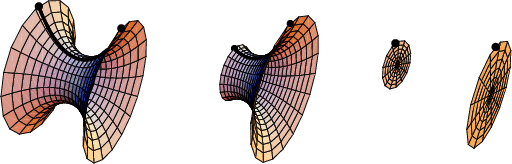
minimal surfaces for several choices of endpoints are shown above. The first two cases are Catenoids,
while the third case is a Goldschmidt Solution.
, this equation has no solutions. The physical interpretation of this fact is that
the surface breaks and forms circular disks in each ring to minimize Area. Calculus of Variations cannot be used
to find such discontinuous solutions (known in this case as Goldschmidt Solutions). The
minimal surfaces for several choices of endpoints are shown above. The first two cases are Catenoids,
while the third case is a Goldschmidt Solution.
To find the maximum value of 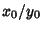 at which Catenary solutions can be obtained, let
at which Catenary solutions can be obtained, let 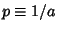 . Then
(31) gives
. Then
(31) gives
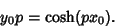 |
(34) |
Now, denote the maximum value of 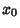 as
as 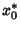 . Then it will be true that
. Then it will be true that 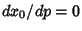 . Take
. Take 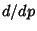 of (34),
of (34),
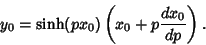 |
(35) |
Now set 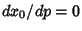
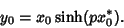 |
(36) |
From (34),
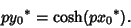 |
(37) |
Take (37) 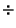 (36),
(36),
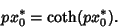 |
(38) |
Defining
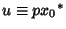 ,
,
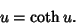 |
(39) |
This has solution
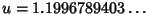 . From (36),
. From (36), 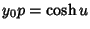 . Divide this by (39) to obtain
. Divide this by (39) to obtain
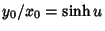 , so the maximum possible value of
, so the maximum possible value of 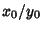 is
is
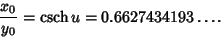 |
(40) |
Therefore, only Goldschmidt ring solutions exist for
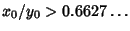 .
.
The Surface Area of the minimal Catenoid surface is given by
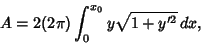 |
(41) |
but since
Some caution is needed in solving (33) for  . If we take
. If we take  and
and 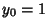 then (33) becomes
then (33) becomes
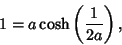 |
(45) |
which has two solutions:
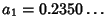 (``deep''), and
(``deep''), and
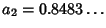 (``flat''). However, upon plugging
these into (44) with
(``flat''). However, upon plugging
these into (44) with 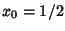 , we find
, we find
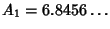 and
and
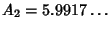 . So
. So 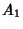 is not, in fact, a
local minimum, and
is not, in fact, a
local minimum, and 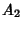 is the only true minimal solution.
is the only true minimal solution.
The Surface Area of the Catenoid solution equals that of the Goldschmidt Solution when (44) equals
the Area of two disks,
![\begin{displaymath}
\pi a^2\left[{\sinh\left({2x_0\over a}\right)+{2x_0\over a}}\right]= 2\pi {y_0}^2
\end{displaymath}](s3_1744.gif) |
(46) |
![\begin{displaymath}
a^2\left[{2\sinh\left({x_0\over a}\right)\cosh\left({x_0\over a}\right)+{2x_0\over a}}\right]-2{y_0}^2=0
\end{displaymath}](s3_1745.gif) |
(47) |
![\begin{displaymath}
a^2\left[{\cosh\left({x_0\over a}\right)\sqrt{\cosh^2\left({x_0\over a}\right)-1}+{x_0\over a}}\right]-{y_0}^2=0.
\end{displaymath}](s3_1746.gif) |
(48) |
Plugging in
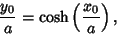 |
(49) |
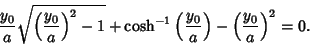 |
(50) |
Defining
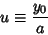 |
(51) |
gives
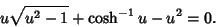 |
(52) |
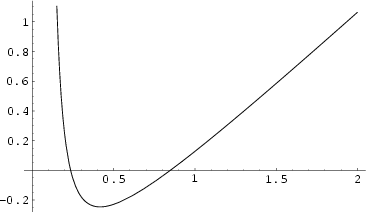
This has a solution
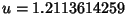 . The value of
. The value of 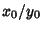 for which
for which
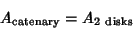 |
(53) |
is therefore
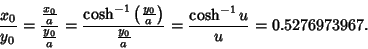 |
(54) |
For
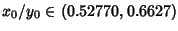 , the Catenary solution has larger Area than the two disks, so it exists only
as a Relative Minimum.
, the Catenary solution has larger Area than the two disks, so it exists only
as a Relative Minimum.
There also exist solutions with a disk (of radius 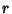 ) between the rings supported by two Catenoids of
revolution. The Area is larger than that for a simple Catenoid, but it is a Relative Minimum. The
equation of the Positive half of this curve is
) between the rings supported by two Catenoids of
revolution. The Area is larger than that for a simple Catenoid, but it is a Relative Minimum. The
equation of the Positive half of this curve is
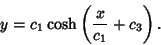 |
(55) |
At 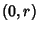 ,
,
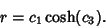 |
(56) |
At 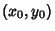 ,
,
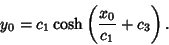 |
(57) |
The Area of the two Catenoids is
Now let
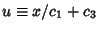 , so
, so 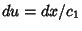
The Area of the central Disk is
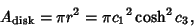 |
(60) |
so the total Area is
![\begin{displaymath}
A = \pi{c_1}^2\left\{{\sinh\left[{2\left({{x_0\over c_1}+c_3...
...eft[{\cosh^2 c_3-\sinh(2c_3)}\right]+{2x_0\over c_1}}\right\}.
\end{displaymath}](s3_1770.gif) |
(61) |
By Plateau's Laws, the Catenoids meet at an Angle of 120°, so
and
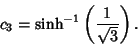 |
(63) |
This means that
so
![\begin{displaymath}
A = \pi{c_1}^2\left\{{\sinh\left[{2\left({{x_0\over c_1}+c_3}\right)}\right]+{2x_0\over c_1}}\right\}.
\end{displaymath}](s3_1779.gif) |
(65) |
Now examine 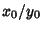 ,
,
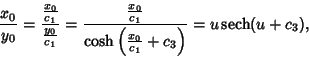 |
(66) |
where
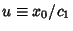 . Finding the maximum ratio of
. Finding the maximum ratio of 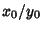 gives
gives
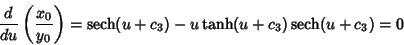 |
(67) |
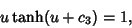 |
(68) |
with
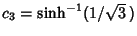 as given above. The solution is
as given above. The solution is
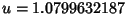 , so the maximum value of
, so the maximum value of 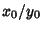 for two
Catenoids with a central disk is
for two
Catenoids with a central disk is
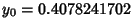 .
.
If we are interested instead in finding the curve from a point 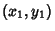 to a point
to a point 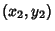 which, when revolved around
the y-Axis (as opposed to the x-Axis), yields a surface of smallest
Surface Area
which, when revolved around
the y-Axis (as opposed to the x-Axis), yields a surface of smallest
Surface Area 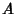 , we proceed as above. Note that the solution is physically equivalent to that for rotation about the
x-Axis, but takes on a different mathematical form. The Area element is
, we proceed as above. Note that the solution is physically equivalent to that for rotation about the
x-Axis, but takes on a different mathematical form. The Area element is
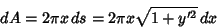 |
(69) |
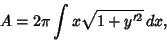 |
(70) |
and the quantity we are minimizing is
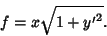 |
(71) |
Taking the derivatives gives
so the Euler-Lagrange Differential Equation becomes
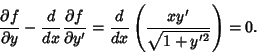 |
(74) |
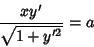 |
(75) |
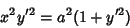 |
(76) |
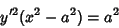 |
(77) |
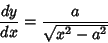 |
(78) |
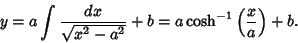 |
(79) |
Solving for 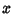 then gives
then gives
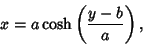 |
(80) |
which is the equation for a Catenary. The Surface Area of the Catenoid product by rotation is
Isenberg (1992, p. 80) discusses finding the Minimal Surface passing through two rings with axes offset from each
other.
See also Apple, Catenoid, Cone Conical Frustum, Cylinder, Darwin-de Sitter Spheroid,
Eight Surface, Gabriel's Horn, Hyperboloid, Lemon, Meridian, Oblate Spheroid,
Pappus's Centroid Theorem, Paraboloid, Parallel (Surface of Revolution), Prolate Spheroid, Pseudosphere,
Sinclair's Soap Film Problem, Solid of Revolution,
Sphere, Spheroid, Toroid, Torus
References
Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 931-937, 1985.
Goldstein, H. Classical Mechanics, 2nd ed. Reading, MA: Addison-Wesley, p. 42, 1980.
Gray, A. ``Surfaces of Revolution.'' Ch. 18 in Modern Differential Geometry of Curves and Surfaces.
Boca Raton, FL: CRC Press, pp. 357-375, 1993.
Isenberg, C. The Science of Soap Films and Soap Bubbles. New York: Dover, pp. 79-80 and Appendix III, 1992.
© 1996-9 Eric W. Weisstein
1999-05-26
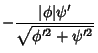
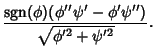
![\begin{displaymath}
\hat {\bf N}(u,v)={\mathop{\rm sgn}\nolimits (\phi)\over\sqr...
...left[{\matrix{\phi'\cos u\cr \psi'\sin u\cr \phi'\cr}}\right],
\end{displaymath}](s3_1672.gif)
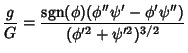
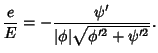
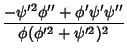
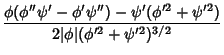
![]() to a point
to a point ![]() which, when
revolved around the x-Axis, yields a surface of smallest Surface Area
which, when
revolved around the x-Axis, yields a surface of smallest Surface Area ![]() (i.e., the Minimal Surface).
This is equivalent to finding the Minimal Surface passing through two circular wire frames. The Area element is
(i.e., the Minimal Surface).
This is equivalent to finding the Minimal Surface passing through two circular wire frames. The Area element is
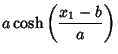
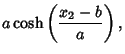
![]() . Without loss of generality, take the origin at the midpoint of the two rings.
Then the two endpoints are located at
. Without loss of generality, take the origin at the midpoint of the two rings.
Then the two endpoints are located at ![]() and
and ![]() , and
, and
![]() at which Catenary solutions can be obtained, let
at which Catenary solutions can be obtained, let ![]() . Then
(31) gives
. Then
(31) gives
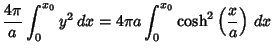
![$\displaystyle 4\pi a \int_0^{x_0} {\textstyle{1\over 2}}\left[{\cosh\left({2x\over a}\right)+1}\right]\, dx$](s3_1729.gif)
![$\displaystyle 2\pi a\left[{\int_0^{x_0}\cosh\left({2x\over a}\right)\, dx + \int_0^{x_0} dx}\right]$](s3_1730.gif)
![$\displaystyle 2\pi a\left[{{a\over 2}\sinh\left({2x\over a}\right)+ x}\right]_0^{x_0}$](s3_1731.gif)
![$\displaystyle \pi a^2\left[{\sinh\left({2x\over a}\right)+ {2x\over a}}\right]_0^{x_0}$](s3_1732.gif)
![$\displaystyle \pi a^2\left[{\sinh\left({2x_0\over a}\right)+ {2x_0\over a}}\right].$](s3_1733.gif)
![]() . If we take
. If we take ![]() and
and ![]() then (33) becomes
then (33) becomes
![]() , the Catenary solution has larger Area than the two disks, so it exists only
as a Relative Minimum.
, the Catenary solution has larger Area than the two disks, so it exists only
as a Relative Minimum.
![]() ) between the rings supported by two Catenoids of
revolution. The Area is larger than that for a simple Catenoid, but it is a Relative Minimum. The
equation of the Positive half of this curve is
) between the rings supported by two Catenoids of
revolution. The Area is larger than that for a simple Catenoid, but it is a Relative Minimum. The
equation of the Positive half of this curve is
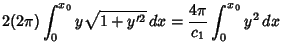
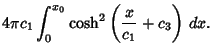
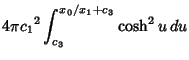
![$\displaystyle 4\pi{c_1}^2 {\textstyle{1\over 2}}\int_{c_3}^{x_0/x_1+c_3} [\cosh(2u)+1]\,du$](s3_1765.gif)
![$\displaystyle 2\pi{c_1}^2\left\{{{\textstyle{1\over 2}}\sinh\left[{2\left({{x_0...
...}+c_3}\right)}\right]-{\textstyle{1\over 2}}\sinh(2c_3)+{x_0\over c_1}}\right\}$](s3_1767.gif)
![$\displaystyle \pi{c_1}^2\left\{{\sinh\left[{2\left({{x_0\over c_1}+c_3}\right)}\right]-\sinh(2c_3)+{2x_0\over c_1}}\right\}.$](s3_1768.gif)
![$\displaystyle \left[{dy\over dx}\right]_{x=0} = \left[{\sinh\left({{x\over c_1}+c_3}\right)}\right]_{x=0}$](s3_1772.gif)
![$\displaystyle [1+\sinh^2 c_3]-2\sinh c_3\sqrt{1+\sinh^2 c_3}$](s3_1776.gif)
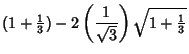
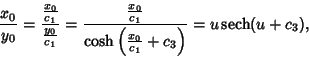
![]() to a point
to a point ![]() which, when revolved around
the y-Axis (as opposed to the x-Axis), yields a surface of smallest
Surface Area
which, when revolved around
the y-Axis (as opposed to the x-Axis), yields a surface of smallest
Surface Area ![]() , we proceed as above. Note that the solution is physically equivalent to that for rotation about the
x-Axis, but takes on a different mathematical form. The Area element is
, we proceed as above. Note that the solution is physically equivalent to that for rotation about the
x-Axis, but takes on a different mathematical form. The Area element is
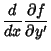
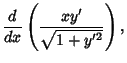
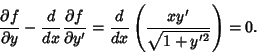

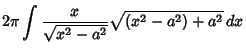
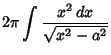
![$\displaystyle \left[{{x\over 2}\sqrt{x^2-a^2}+{a^2\over 2}\ln\left({x+\sqrt{x^2-a^2}\,}\right)}\right]^{x_2}_{x_1}$](s3_1803.gif)
![$\displaystyle {1\over 2}\left[{x_2\sqrt{{x_2}^2-a^2}-x_1\sqrt{{x_1}^2-a^2}+a^2\ln\left({x_2+\sqrt{{x_2}^2-a^2}\over x_1+\sqrt{{x_1}^2-a^2}\,}\right)}\right].$](s3_1804.gif)