|
|
|
|
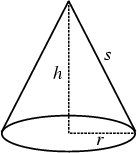
A cone is a Pyramid with a circular Cross-Section. A right cone is a cone with its vertex above the center of
its base. A right cone of height ![]() can be described by the parametric equations
can be described by the parametric equations
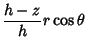 |
(1) | ||
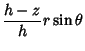 |
(2) | ||
| (3) |
| (4) |
| (5) |
The Centroid can be obtained by setting ![]() in the equation for the centroid of the
Conical Frustum,
in the equation for the centroid of the
Conical Frustum,
| (6) |
| (7) |
For a right circular cone, the Slant Height ![]() is
is
| (8) |
| (9) |
The Locus of the apex of a variable cone containing an Ellipse fixed in 3-space is a Hyperbola through the Foci of the Ellipse. In addition, the Locus of the apex of a cone containing that Hyperbola is the original Ellipse. Furthermore, the Eccentricities of the Ellipse and Hyperbola are reciprocals.
See also Conic Section, Conical Frustum, Cylinder, Nappe, Pyramid, Sphere
References
Beyer, W. H. (Ed.) CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, pp. 129 and 133, 1987.
Dunham, W. Journey Through Genius: The Great Theorems of Mathematics. New York: Wiley, pp. 76-77, 1990.
Yates, R. C. ``Cones.'' A Handbook on Curves and Their Properties. Ann Arbor, MI: J. W. Edwards, pp. 34-35, 1952.
|
|
|
© 1996-9 Eric W. Weisstein