Hyperbola

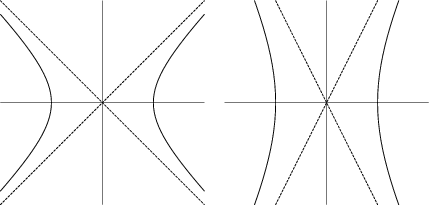
In general, a hyperbola is defined as the Locus of all points in the Plane the difference of whose distances from two fixed points (the Foci $F_1$ and $F_2$) separated by a distance $2c$, where

$$c\equiv \sqrt{a^2+b^2},$$ (1)

is a given Positive constant. By analogy with the definition of the Ellipse, the equation for a hyperbola with Semimajor Axis $a$ parallel to the x-Axis and Semiminor Axis $b$ parallel to the y-Axis is given by

$${(x-x_0)^2\over a^2} - {(y-y_0)^2\over b^2} = 1.$$ (2)

Unlike the Ellipse, no points of the hyperbola actually lie on the Semiminor Axis, but rather the ratio $b/a$ determined the vertical scaling of the hyperbola. The Eccentricity of the hyperbola is defined as

$$e\equiv {c\over a} = \sqrt{1+{b^2\over a^2}}.$$ (3)

In the standard equation of the hyperbola, the center is located at $(x_0,y_0)$, the Foci are at $(x_0\pm c,y_0)$, and the vertices are at $(x_0\pm a,y_0)$. The so-called Asymptotes (shown as the dashed lines in the above figures) can be found by substituting 0 for the 1 on the right side of the general equation (2),

$$y=\pm{b\over a}(x-x_0)+y_0,$$ (4)

and therefore have Slopes $\pm b/a$.

The special case $a=b$ (the left diagram above) is known as a Right Hyperbola because the Asymptotes are Perpendicular.

In Polar Coordinates, the equation of a hyperbola centered at the Origin (i.e., with $x_0=y_0=0$) is

$$r^2={a^2b^2\over b^2\cos^2\theta-a^2\sin^2\theta}.$$ (5)

In Polar Coordinates centered at a Focus,

$$r = {a(e^2-1)\over 1-e\cos\theta}.$$ (6)

The two-center Bipolar Coordinates equation with origin at a Focus is

$$r_1-r_2=\pm 2a.$$ (7)

The parametric equations for the hyperbola are

$$x = \pm a\cosh t$$ (8)

$$y = b\sinh t.$$ (9)

The Curvature and Tangential Angle are

$$\kappa(t) = -[\cosh(2t)]^{-3/2}$$ (10)

$$\phi(t) = -\tan^{-1}(\tanh t).$$ (11)

The special case of the Right Hyperbola was first studied by Menaechmus. Euclid and Aristaeus wrote about the general hyperbola, but only studied one branch of it. The hyperbola was given its present name by Apollonius, who was the first to study both branches. The Focus and Directrix were considered by Pappus (MacTutor Archive). The hyperbola is the shape of an orbit of a body on an escape trajectory (i.e., a body with positive energy), such as some comets, about a fixed mass, such as the sun.

The Locus of the apex of a variable Cone containing an Ellipse fixed in 3-space is a hyperbola through the Foci of the Ellipse. In addition, the Locus of the apex of a Cone containing that hyperbola is the original Ellipse. Furthermore, the Eccentricities of the Ellipse and hyperbola are reciprocals.

See also Conic Section, Ellipse, Hyperboloid, Jerabek's Hyperbola, Kiepert's Hyperbola, Parabola, Quadratic Curve, Rectangular Hyperbola, Reflection Property, Right Hyperbola

References

Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, pp. 199-200, 1987.

Casey, J. ``The Hyperbola.'' Ch. 7 in A Treatise on the Analytical Geometry of the Point, Line, Circle, and Conic Sections, Containing an Account of Its Most Recent Extensions, with Numerous Examples, 2nd ed., rev. enl. Dublin: Hodges, Figgis, & Co., pp. 250-284, 1893.

Courant, R. and Robbins, H. What is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed. Oxford, England: Oxford University Press, pp. 75-76, 1996.

Lawrence, J. D. A Catalog of Special Plane Curves. New York: Dover, pp. 79-82, 1972.

Lee, X. ``Hyperbola.'' http://www.best.com/~xah/SpecialPlaneCurves_dir/Hyperbola_dir/hyperbola.html.

Lockwood, E. H. ``The Hyperbola.'' Ch. 3 in A Book of Curves. Cambridge, England: Cambridge University Press, pp. 24-33, 1967.

MacTutor History of Mathematics Archive. ``Hyperbola.'' http://www-groups.dcs.st-and.ac.uk/~history/Curves/Hyperbola.html.