A quantity defined for a Conic Section which can be given in terms of Semimajor and
Semiminor Axes for an Ellipse. For an Ellipse with Semimajor Axis 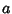 and
Semiminor Axis
and
Semiminor Axis 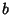 ,
,
The eccentricity can be interpreted as the fraction of the distance to the semimajor axis at which the
Focus lies,
where 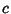 is the distance from the center of the Conic Section to the Focus.
The table below gives the type of Conic Section corresponding to various ranges of eccentricity
is the distance from the center of the Conic Section to the Focus.
The table below gives the type of Conic Section corresponding to various ranges of eccentricity 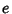 .
.
See also Circle, Conic Section, Eccentric Anomaly, Ellipse, Flattening, Hyperbola,
Oblateness, Parabola, Semimajor Axis, Semiminor Axis
© 1996-9 Eric W. Weisstein
1999-05-25
![]() and
Semiminor Axis
and
Semiminor Axis ![]() ,
,