|
|
|
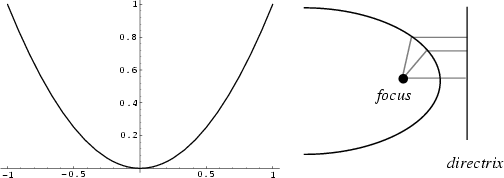
The set of all points in the Plane equidistant from a given Line (the Directrix) and a given point not on the line (the Focus).
The parabola was studied by Menaechmus in an attempt to achieve Cube Duplication. Menaechmus solved the problem by
finding the intersection of the two parabolas ![]() and
and ![]() . Euclid
. Euclid ![]() wrote about the parabola, and it was
given its present name by Apollonius.
wrote about the parabola, and it was
given its present name by Apollonius. ![]() Pascal
Pascal ![]() considered the parabola as a projection of a
Circle, and Galileo
considered the parabola as a projection of a
Circle, and Galileo ![]() showed that projectiles falling under uniform gravity
showed that projectiles falling under uniform gravity ![]() follow
parabolic paths. Gregory
follow
parabolic paths. Gregory ![]() and Newton
and Newton ![]() considered the Catacaustic properties of a parabola which
bring parallel rays of light to a focus
considered the Catacaustic properties of a parabola which
bring parallel rays of light to a focus ![]() (MacTutor Archive).
(MacTutor Archive).
For a parabola opening to the right, the equation in Cartesian Coordinates is
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
| (9) | |||
| (10) |

The Curvature, Arc Length, and Tangential Angle are
| (11) | |||
| (12) | |||
| (13) |
The Tangent Vector of the parabola is
| (14) | |||
| (15) |
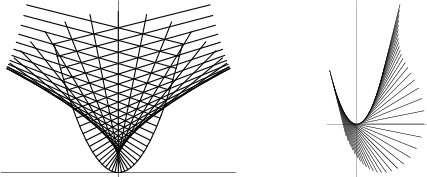
See also Conic Section, Ellipse, Hyperbola, Quadratic Curve, Reflection Property, Tschirnhausen Cubic Pedal Curve
References
Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 198, 1987.
Casey, J. ``The Parabola.'' Ch. 5 in
A Treatise on the Analytical Geometry of the Point, Line, Circle, and Conic Sections, Containing
an Account of Its Most Recent Extensions, with Numerous Examples, 2nd ed., rev. enl. Dublin: Hodges, Figgis, & Co., pp. 173-200, 1893.
Coxeter, H. S. M. ``Conics.'' §8.4 in Introduction to Geometry, 2nd ed.
New York: Wiley, pp. 115-119, 1969.
Lawrence, J. D. A Catalog of Special Plane Curves. New York: Dover, pp. 67-72, 1972.
Lee, X. ``Parabola.''
http://www.best.com/~xah/SpecialPlaneCurves_dir/Parabola_dir/parabola.html.
Lockwood, E. H. ``The Parabola.'' Ch. 1 in A Book of Curves. Cambridge, England: Cambridge University Press,
pp. 2-12, 1967.
MacTutor History of Mathematics Archive. ``Parabola.''
http://www-groups.dcs.st-and.ac.uk/~history/Curves/Parabola.html.
Pappas, T. ``The Parabolic Ceiling of the Capitol.'' The Joy of Mathematics. San Carlos, CA: Wide World Publ./Tetra,
pp. 22-23, 1989.
|
|
|
© 1996-9 Eric W. Weisstein