|
|
|
|
A cylinder is a solid of circular Cross-Section in which the centers of the Circles all lie on a
single Line. The cylinder was extensively studied by Archimedes ![]() in his 2-volume work On the Sphere
and Cylinder in ca. 225 BC.
in his 2-volume work On the Sphere
and Cylinder in ca. 225 BC. ![]()
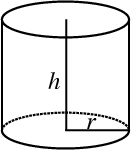
A cylinder is called a right cylinder if it is ``straight'' in the sense that its cross-sections lie directly on top of
each other; otherwise, the cylinder is called oblique. The surface of a cylinder of height ![]() and Radius
and Radius ![]() can be
described parametrically by
can be
described parametrically by
| (1) | |||
| (2) | |||
| (3) |
| (4) | |||
| (5) |
| (6) |
See also Cone, Cylinder-Sphere Intersection, Cylindrical Segment, Elliptic Cylinder, Generalized Cylinder, Sphere, Steinmetz Solid, Viviani's Curve
References
Beyer, W. H. (Ed.) CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press,
p. 129, 1987.
|
|
|
© 1996-9 Eric W. Weisstein