|
|
|
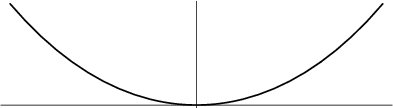
The curve a hanging flexible wire or chain assumes when supported at its ends and acted upon by a uniform gravitational
force. The word catenary is derived from the Latin word for ``chain.'' In 1669, Jungius disproved
Galileo's ![]() claim that the curve of a chain hanging under gravity would be a Parabola
(MacTutor Archive). The curve is also called the Alysoid and Chainette. The equation was obtained
by Leibniz,
claim that the curve of a chain hanging under gravity would be a Parabola
(MacTutor Archive). The curve is also called the Alysoid and Chainette. The equation was obtained
by Leibniz, ![]() Huygens,
Huygens, ![]() and Johann Bernoulli
and Johann Bernoulli ![]() in 1691 in
response to a challenge by Jakob Bernoulli.
in 1691 in
response to a challenge by Jakob Bernoulli. ![]()
Huygens ![]() was the first to use the term catenary in a letter to Leibniz
was the first to use the term catenary in a letter to Leibniz ![]() in 1690, and David Gregory
in 1690, and David Gregory ![]() wrote a treatise on the catenary in 1690 (MacTutor Archive). If you roll a Parabola along a straight line, its
Focus traces out a catenary. As proved by Euler
wrote a treatise on the catenary in 1690 (MacTutor Archive). If you roll a Parabola along a straight line, its
Focus traces out a catenary. As proved by Euler ![]() in 1744, the catenary is also the curve which, when rotated,
gives the surface of minimum Surface Area (the Catenoid) for the given bounding Circle.
in 1744, the catenary is also the curve which, when rotated,
gives the surface of minimum Surface Area (the Catenoid) for the given bounding Circle.
The parametric equations for the catenary are given by
| (1) | |||
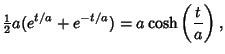 |
(2) |
| (3) |

The Arc Length, Curvature, and Tangential Angle are
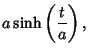 |
(4) | ||
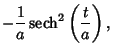 |
(5) | ||
![$\displaystyle -2\tan^{-1}\left[{\tanh\left({t\over 2a}\right)}\right].$](c1_546.gif) |
(6) |
See also Calculus of Variations, Catenoid, Lindelof's Theorem, Surface of Revolution
References
Geometry Center. ``The Catenary.''
http://www.geom.umn.edu/zoo/diffgeom/surfspace/catenoid/catenary.html.
Gray, A. ``The Evolute of a Tractrix is a Catenary.'' §5.3 in
Modern Differential Geometry of Curves and Surfaces.
Boca Raton, FL: CRC Press, pp. 80-81, 1993.
Lawrence, J. D. A Catalog of Special Plane Curves. New York: Dover, pp. 195 and 199-200, 1972.
Lockwood, E. H. ``The Tractrix and Catenary.'' Ch. 13 in A Book of Curves. Cambridge, England:
Cambridge University Press, pp. 118-124, 1967.
MacTutor History of Mathematics Archive. ``Catenary.''
http://www-groups.dcs.st-and.ac.uk/~history/Curves/Catenary.html.
Pappas, T. ``The Catenary & the Parabolic Curves.'' The Joy of Mathematics. San Carlos, CA: Wide World Publ./Tetra,
p. 34, 1989.
Yates, R. C. ``Catenary.'' A Handbook on Curves and Their Properties. Ann Arbor, MI: J. W. Edwards, pp. 12-14, 1952.
|
|
|
© 1996-9 Eric W. Weisstein