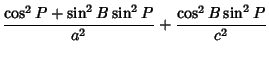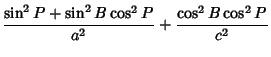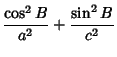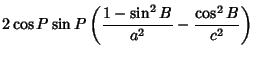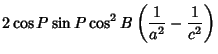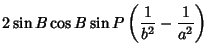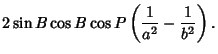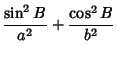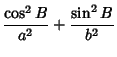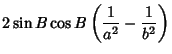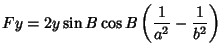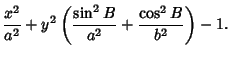A ``squashed'' Spheroid for which the equatorial radius 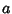 is greater than the polar radius
is greater than the polar radius 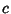 , so
, so 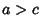 . To
first approximation, the shape assumed by a rotating fluid (including the Earth,
. To
first approximation, the shape assumed by a rotating fluid (including the Earth,  which is ``fluid'' over
astronomical time scales) is an oblate spheroid. The oblate spheroid can be specified parametrically by the usual
Spheroid equations (for a Spheroid with z-Axis as the symmetry axis),
which is ``fluid'' over
astronomical time scales) is an oblate spheroid. The oblate spheroid can be specified parametrically by the usual
Spheroid equations (for a Spheroid with z-Axis as the symmetry axis),
with 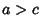 ,
, 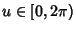 , and
, and ![$v\in[0, \pi]$](o_14.gif) . Its Cartesian equation is
. Its Cartesian equation is
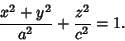 |
(4) |
The Ellipticity of an oblate spheroid is defined by
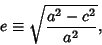 |
(5) |
so that
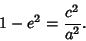 |
(6) |
Then the radial distance from the rotation axis is given by
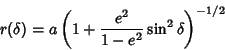 |
(7) |
as a function of the Latitude 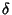 .
.
The Surface Area and Volume of an oblate spheroid are
An oblate spheroid with its origin at a Focus has equation
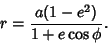 |
(10) |
Define 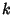 and expand up to Powers of
and expand up to Powers of 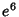 ,
,
Expanding 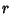 in Powers of Ellipticity to
in Powers of Ellipticity to 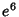 therefore yields
therefore yields
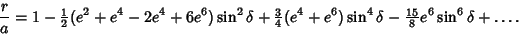 |
(14) |
In terms of Legendre Polynomials,
The Ellipticity may also be expressed in terms of the Oblateness (also called Flattening), denoted
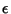 or
or 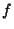 .
.
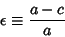 |
(16) |
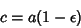 |
(17) |
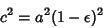 |
(18) |
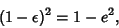 |
(19) |
so
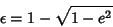 |
(20) |
and
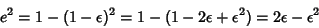 |
(21) |
![\begin{displaymath}
r = a\left[{1 + {2\epsilon -\epsilon^2\over (1-\epsilon)^2} \sin^2\delta}\right]^{-1/2}.
\end{displaymath}](o_50.gif) |
(22) |
Define 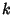 and expand up to Powers of
and expand up to Powers of 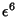
Expanding 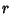 in Powers of the Oblateness to
in Powers of the Oblateness to 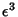 yields
yields
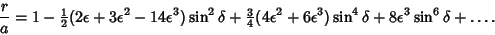 |
(26) |
In terms of Legendre Polynomials,
To find the projection of an oblate spheroid onto a Plane, set up a coordinate system such that the z-Axis is
towards the observer, and the 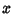 -axis is in the Plane of the page. The equation for an oblate spheroid is
-axis is in the Plane of the page. The equation for an oblate spheroid is
![\begin{displaymath}
r(\theta)=a\left[{1+{2\epsilon-\epsilon^2 \over (1-\epsilon)^2}\cos^2\theta}\right]^{-1/2}.
\end{displaymath}](o_62.gif) |
(28) |
Define
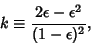 |
(29) |
and
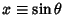 . Then
. Then
![\begin{displaymath}
r(\theta) =a[1+k(1-x^2)]^{-1/2} = a(1+k-kx^2)^{-1/2}.
\end{displaymath}](o_65.gif) |
(30) |
Now rotate that spheroid about the 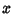 -axis by an Angle
-axis by an Angle 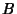 so that the new symmetry axes for the spheroid are
so that the new symmetry axes for the spheroid are 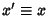 ,
, 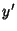 , and
, and 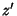 . The projected height of a point in the
. The projected height of a point in the 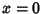 Plane on the
Plane on the 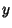 -axis is
-axis is
To find the highest projected point,
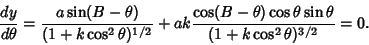 |
(32) |
Simplifying,
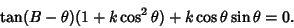 |
(33) |
But
Plugging (34) into (33),
![\begin{displaymath}
{\sqrt{1-x^2}\tan B-x \over\sqrt{1-x^2}+x\tan B} [1+k(1-x^2)]+kx\sqrt{1-x^2} = 0
\end{displaymath}](o_79.gif) |
(35) |
and performing a number of algebraic simplifications
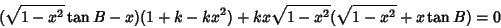 |
(36) |
![$[(1+k)\sqrt{1-x^2}\tan B-k x^2\sqrt{1-x^2}\tan B-x-kx+kx^3]$](o_81.gif)
|
|
![$ +[kx(1-x^2)+kx^2\sqrt{1-x^2}\tan B]\quad$](o_82.gif)
|
(37) |
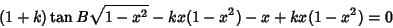 |
(38) |
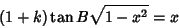 |
(39) |
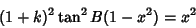 |
(40) |
![\begin{displaymath}
x^2[1+(1+k)^2\tan^2 B]=(1+k)^2\tan^2 B
\end{displaymath}](o_86.gif) |
(41) |
finally gives the expression for 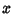 in terms of
in terms of 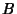 and
and 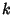 ,
,
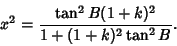 |
(42) |
Combine (30) and (31) and plug in for 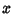 ,
,
Now re-express 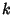 in terms of
in terms of 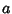 and
and 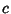 , using
, using
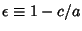 ,
,
so
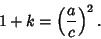 |
(45) |
Plug (44) and (45) into (43) to obtain the
Semiminor Axis of the projected oblate spheroid,
We wish to find the equation for a spheroid which has been rotated about the 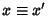 -axis by Angle
-axis by Angle 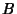 , then the
, then the
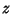 -axis by Angle
-axis by Angle 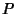
Now, in the original coordinates 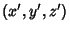 , the spheroid is given by the equation
, the spheroid is given by the equation
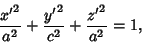 |
(48) |
which becomes in the new coordinates,
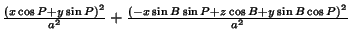
|
|
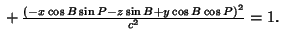
|
(49) |
Collecting Coefficients,
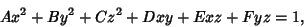 |
(50) |
where
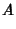 |
 |
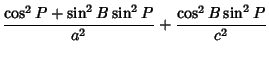 |
(51) |
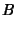 |
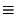 |
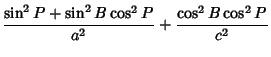 |
(52) |
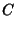 |
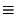 |
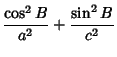 |
(53) |
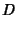 |
 |
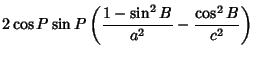 |
|
| |
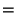 |
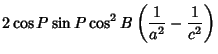 |
(54) |
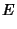 |
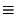 |
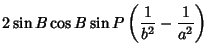 |
(55) |
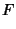 |
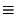 |
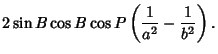 |
(56) |
If we are interested in computing 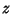 , the radial distance from the symmetry axis of the spheroid (
, the radial distance from the symmetry axis of the spheroid (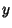 ) corresponding to
a point
) corresponding to
a point
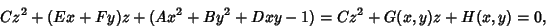 |
(57) |
where
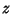 can now be computed using the quadratic equation when
can now be computed using the quadratic equation when 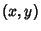 is given,
is given,
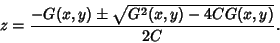 |
(60) |
If 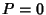 , then we have
, then we have 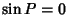 and
and 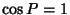 , so (51) to (56) and
(58) to (59) become
, so (51) to (56) and
(58) to (59) become
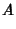 |
 |
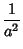 |
(61) |
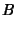 |
 |
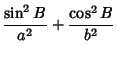 |
(62) |
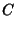 |
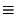 |
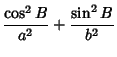 |
(63) |
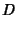 |
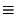 |
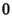 |
(64) |
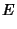 |
 |
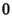 |
(65) |
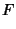 |
 |
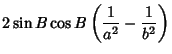 |
(66) |
 |
 |
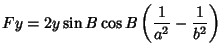 |
(67) |
 |
 |
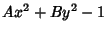 |
|
| |
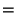 |
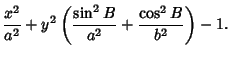 |
(68) |
See also Darwin-de Sitter Spheroid, Ellipsoid, Oblate Spheroidal Coordinates, Prolate Spheroid,
Sphere, Spheroid
References
Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 131, 1987.
© 1996-9 Eric W. Weisstein
1999-05-26
![]() is greater than the polar radius
is greater than the polar radius ![]() , so
, so ![]() . To
first approximation, the shape assumed by a rotating fluid (including the Earth,
. To
first approximation, the shape assumed by a rotating fluid (including the Earth, ![]() which is ``fluid'' over
astronomical time scales) is an oblate spheroid. The oblate spheroid can be specified parametrically by the usual
Spheroid equations (for a Spheroid with z-Axis as the symmetry axis),
which is ``fluid'' over
astronomical time scales) is an oblate spheroid. The oblate spheroid can be specified parametrically by the usual
Spheroid equations (for a Spheroid with z-Axis as the symmetry axis),
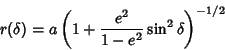
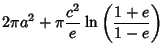
![]() and expand up to Powers of
and expand up to Powers of ![]() ,
,
![\begin{displaymath}
r = a\left[{1 + {2\epsilon -\epsilon^2\over (1-\epsilon)^2} \sin^2\delta}\right]^{-1/2}.
\end{displaymath}](o_50.gif)
![]() -axis is in the Plane of the page. The equation for an oblate spheroid is
-axis is in the Plane of the page. The equation for an oblate spheroid is
![\begin{displaymath}
r(\theta)=a\left[{1+{2\epsilon-\epsilon^2 \over (1-\epsilon)^2}\cos^2\theta}\right]^{-1/2}.
\end{displaymath}](o_62.gif)
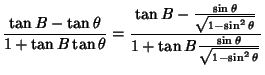
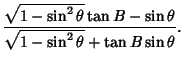
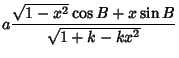
![$\displaystyle a {\cos B+(1+k){\sin^2 B\over\cos B}\over \sqrt{(1+k)[1+(1+k)\tan^2 B]}}$](o_89.gif)
![$\displaystyle a {\cos^2 B+(1+k)\sin^2 B\over\cos B\sqrt{(1+k)[1+(1+k)\tan^2 B]}}.$](o_90.gif)
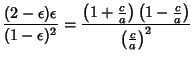
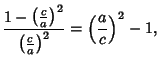
![$\displaystyle a {\cos^2 B+\left({a\over c}\right)^2\sin^2 B \over \cos B \sqrt{\left({a\over c}\right)^2\left[{1+\left({a\over c}\right)^2\tan^2 B}\right]}}$](o_96.gif)
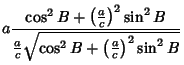
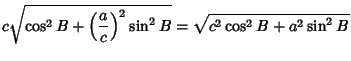
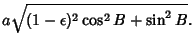
![]() -axis by Angle
-axis by Angle ![]() , then the
, then the
![]() -axis by Angle
-axis by Angle ![]()
![$\displaystyle \left[\begin{array}{ccc}1 & 0 & 0 \\ 0 & \cos B & \sin B \\ 0 &...
... & \cos P \end{array}\right]\left[\begin{array}{c}x\\ y\\ z\end{array}\right]$](o_104.gif)
![$\displaystyle \left[\begin{array}{ccc}\cos P & 0 & \sin P \\ -\sin B \sin P & ...
...s B\cos P\end{array}\right]\left[\begin{array}{c}x\\ y\\ z\end{array}\right].$](o_105.gif)