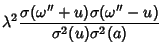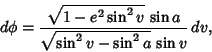The Geodesic on an Oblate Spheroid can be computed analytically for a spheroid specified parametrically
by
with 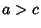 , although it is much more unwieldy than for a simple Sphere.
Using the first Partial Derivatives
, although it is much more unwieldy than for a simple Sphere.
Using the first Partial Derivatives
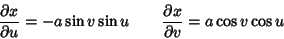 |
(4) |
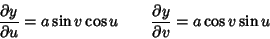 |
(5) |
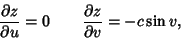 |
(6) |
and second Partial Derivatives
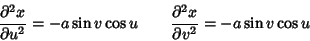 |
(7) |
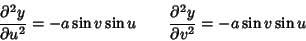 |
(8) |
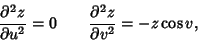 |
(9) |
gives the Geodesics functions as
Since 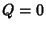 and
and 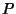 and
and 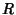 are explicit functions of
are explicit functions of 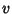 only, we can use the special form of the Geodesic
equation.
only, we can use the special form of the Geodesic
equation.
Integrating gives
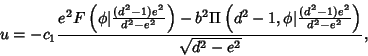 |
(14) |
where
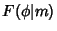 is an Elliptic Integral of the First Kind with Parameter
is an Elliptic Integral of the First Kind with Parameter 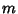 , and
, and
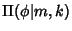 is
an Elliptic Integral of the Third Kind.
is
an Elliptic Integral of the Third Kind.
Geodesics other than Meridians of an Oblate Spheroid undulate between two
parallels with latitudes equidistant from the equator. Using the Weierstraß Sigma Function and Weierstraß Zeta Function, the Geodesic on the Oblate
Spheroid can be written as
(Forsyth 1960, pp. 108-109; Halphen 1886-1891).
The equation of the Geodesic can be put in the form
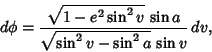 |
(20) |
where 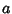 is the smallest value of
is the smallest value of 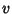 on the curve. Furthermore, the difference in longitude between points of
highest and next lowest latitude on the curve is
on the curve. Furthermore, the difference in longitude between points of
highest and next lowest latitude on the curve is
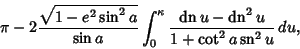 |
(21) |
where the Modulus of the
Elliptic Function is
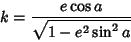 |
(22) |
(Forsyth 1960, p. 446).
See also Ellipsoid Geodesic, Oblate Spheroid, Sphere Geodesic
References
Forsyth, A. R. Calculus of Variations. New York: Dover, 1960.
Halphen, G. H. Traité des fonctions elliptiques et de leurs applications fonctions elliptiques, Vol. 2.
Paris: Gauthier-Villars, pp. 238-243, 1886-1891.
© 1996-9 Eric W. Weisstein
1999-05-26
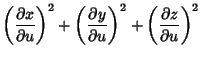
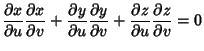
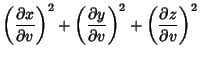
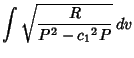

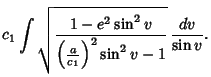
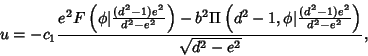
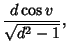
![$\displaystyle \kappa {\sigma(a+u)\over\sigma(u)\sigma(a)} e^{u[\eta-\zeta(\omega+a)]}$](o_173.gif)
![$\displaystyle \kappa {\sigma(a-u)\over\sigma(u)\sigma(a)} e^{-u[\eta-\zeta(\omega+a)]}$](o_175.gif)