|
|
|
A Quadratic Surface which is given in Cartesian Coordinates by
| (1) |
| (2) |
| (3) | |||
| (4) | |||
| (5) |
| (6) |
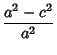 |
(7) | ||
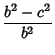 |
(8) | ||
| (9) |
| (10) |
| (11) |
A different parameterization of the ellipsoid is the so-called stereographic ellipsoid, given by the parametric equations
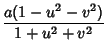 |
(12) | ||
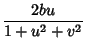 |
(13) | ||
| (14) |
A third parameterization is the Mercator parameterization
| (15) | |||
| (16) | |||
| (17) |
The Support Function of the ellipsoid is
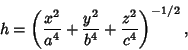 |
(18) |
| (19) |
See also Convex Optimization Theory, Oblate Spheroid, Prolate Spheroid, Sphere, Spheroid
References
Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 131, 1987.
Bowman, F. Introduction to Elliptic Functions, with Applications. New York: Dover, 1961.
Fischer, G. (Ed.). Plate 65 in Mathematische Modelle/Mathematical Models, Bildband/Photograph Volume.
Braunschweig, Germany: Vieweg, p. 60, 1986.
Gray, A. ``The Ellipsoid'' and ``The Stereographic Ellipsoid.'' §11.2 and 11.3 in
Modern Differential Geometry of Curves and Surfaces. Boca Raton, FL: CRC Press, pp. 215-217, and 296, 1993.
|
|
|
© 1996-9 Eric W. Weisstein