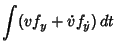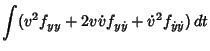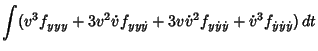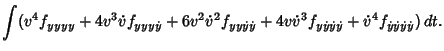A fundamental equation of Calculus of Variations which states that if 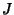 is defined by an Integral of the form
is defined by an Integral of the form
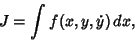 |
(1) |
where
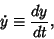 |
(2) |
then 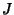 has a Stationary Value if the Euler-Lagrange differential equation
has a Stationary Value if the Euler-Lagrange differential equation
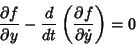 |
(3) |
is satisfied. If time Derivative Notation is replaced instead by space variable notation, the
equation becomes
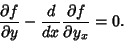 |
(4) |
In many physical problems, 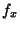 (the Partial Derivative of
(the Partial Derivative of 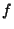 with respect to
with respect to 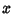 ) turns out to be 0, in
which case a manipulation of the Euler-Lagrange differential equation reduces to the greatly simplified and
partially integrated form known as the Beltrami Identity,
) turns out to be 0, in
which case a manipulation of the Euler-Lagrange differential equation reduces to the greatly simplified and
partially integrated form known as the Beltrami Identity,
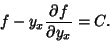 |
(5) |
For three independent variables (Arfken 1985, pp. 924-944), the equation generalizes to
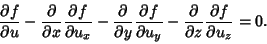 |
(6) |
Problems in the Calculus of Variations often can be solved by solution of the appropriate Euler-Lagrange equation.
To derive the Euler-Lagrange differential equation, examine
since
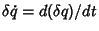 . Now, integrate the second term by Parts using
. Now, integrate the second term by Parts using
so
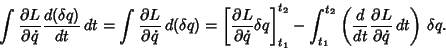 |
(10) |
Combining (7) and (10) then gives
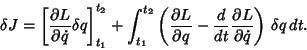 |
(11) |
But we are varying the path only, not the endpoints, so
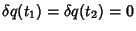 and (11) becomes
and (11) becomes
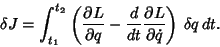 |
(12) |
We are finding the Stationary Values such that 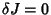 . These must vanish for any small
change
. These must vanish for any small
change 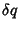 , which gives from (12),
, which gives from (12),
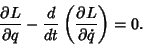 |
(13) |
This is the Euler-Lagrange differential equation.
The variation in 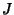 can also be written in terms of the parameter
can also be written in terms of the parameter 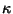 as
as
where
and the first, second, etc., variations are
The second variation can be re-expressed using
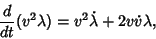 |
(21) |
so
![\begin{displaymath}
I_2+[v^2\lambda]_2^1=\int_1^2 [v^2(f_{yy}+\dot\lambda)+2v\dot v(f_{y\dot y}+\lambda)+{\dot v}^2f_{\dot y\dot y}]\,dt.
\end{displaymath}](e_2188.gif) |
(22) |
But
![\begin{displaymath}[v^2\lambda]_2^1=0.
\end{displaymath}](e_2189.gif) |
(23) |
Now choose 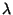 such that
such that
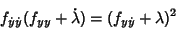 |
(24) |
and 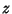 such that
such that
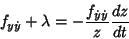 |
(25) |
so that 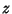 satisfies
satisfies
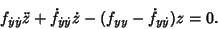 |
(26) |
It then follows that
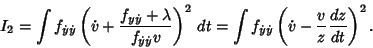 |
(27) |
See also Beltrami Identity, Brachistochrone Problem, Calculus of Variations,
Euler-Lagrange Derivative
References
Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, 1985.
Forsyth, A. R. Calculus of Variations. New York: Dover, pp. 17-20 and 29, 1960.
Morse, P. M. and Feshbach, H. ``The Variational Integral and the Euler Equations.'' §3.1 in
Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 276-280, 1953.
© 1996-9 Eric W. Weisstein
1999-05-25
![]() is defined by an Integral of the form
is defined by an Integral of the form
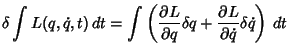
![$\displaystyle \int \left[{{\partial L\over \partial q}\,\delta q+{\partial L\over \partial \dot q} {d(\delta q)\over dt}}\right]\,dt,$](e_2163.gif)
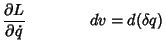
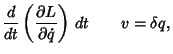
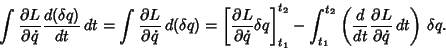
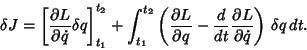
![]() can also be written in terms of the parameter
can also be written in terms of the parameter ![]() as
as
![$\displaystyle \int [f(x,y+\kappa v,\dot y+\kappa\dot v)-f(x,y,\dot y)]\,dt$](e_2174.gif)