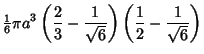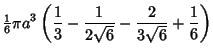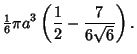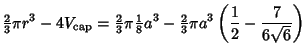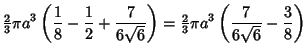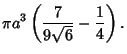A square pyramid is a Pyramid with a Square base. If the top of the pyramid is cut off by a Plane, a
square Pyramidal Frustum is obtained. If the four Triangles of the square pyramid are
Equilateral, the square pyramid is the ``regular'' Polyhedron known as Johnson
Solid 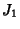 and, for side length
and, for side length 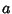 , has height
, has height
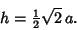 |
(1) |
Using the equation for a general Pyramid, the Volume
of the ``regular'' is therefore
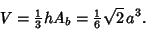 |
(2) |
If the apex of the pyramid does not lie atop the center of the base, then the
Slant Height is given by
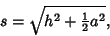 |
(3) |
where 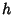 is the height and
is the height and 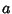 is the length of a side of the base.
is the length of a side of the base.
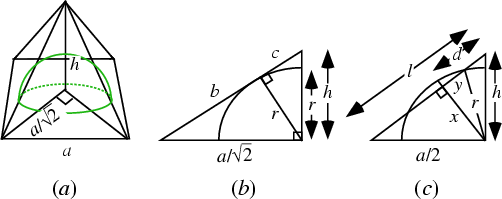
Consider a Hemisphere placed on the base of a square pyramid (having side lengths 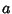 and height
and height 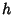 ). Further, let the
hemisphere be tangent to the four apex edges. Then what is the volume of the Hemisphere which is interior the
pyramid (Cipra 1993)?
). Further, let the
hemisphere be tangent to the four apex edges. Then what is the volume of the Hemisphere which is interior the
pyramid (Cipra 1993)?
From Fig. (a), the Circumradius of the base is 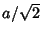 . Now find
. Now find 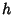 in terms of
in terms of 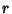 and
and 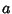 . Fig. (b) shows a
Cross-Section cut by the plane through the pyramid's apex, one of the base's vertices, and the base center. This figure
gives
. Fig. (b) shows a
Cross-Section cut by the plane through the pyramid's apex, one of the base's vertices, and the base center. This figure
gives
so the Slant Height is
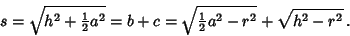 |
(6) |
Solving for 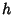 gives
gives
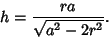 |
(7) |
We know, however, that the Hemisphere must be tangent to the sides, so 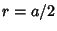 , and
, and
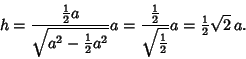 |
(8) |
Fig. (c) shows a Cross-Section through the center, apex, and midpoints of opposite sides. The Pythagorean Theorem
once again gives
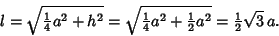 |
(9) |
We now need to find 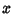 and
and 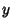 .
.
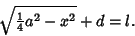 |
(10) |
But we know 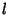 and
and 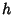 , and
, and 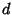 is given by
is given by
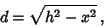 |
(11) |
so
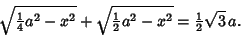 |
(12) |
Solving gives
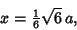 |
(13) |
so
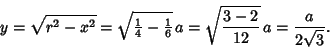 |
(14) |
We can now find the Area of the Spherical Cap as
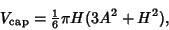 |
(15) |
where
so
Therefore, the volume within the pyramid is
This problem appeared in the Japanese scholastic aptitude test (Cipra 1993).
See also Square Pyramidal Number
References
Cipra, B. ``An Awesome Look at Japan Math SAT.'' Science 259, 22, 1993.
© 1996-9 Eric W. Weisstein
1999-05-26
![]() and, for side length
and, for side length ![]() , has height
, has height
![]() and height
and height ![]() ). Further, let the
hemisphere be tangent to the four apex edges. Then what is the volume of the Hemisphere which is interior the
pyramid (Cipra 1993)?
). Further, let the
hemisphere be tangent to the four apex edges. Then what is the volume of the Hemisphere which is interior the
pyramid (Cipra 1993)?
![]() . Now find
. Now find ![]() in terms of
in terms of ![]() and
and ![]() . Fig. (b) shows a
Cross-Section cut by the plane through the pyramid's apex, one of the base's vertices, and the base center. This figure
gives
. Fig. (b) shows a
Cross-Section cut by the plane through the pyramid's apex, one of the base's vertices, and the base center. This figure
gives
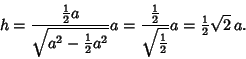
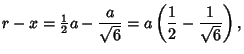
![$\displaystyle {\textstyle{1\over 6}} \pi a^3 \left[{3\left({1\over 12}\right)+\...
...}-{1\over\sqrt{6}}}\right)^2}\right]
\left({{1\over 2}-{1\over\sqrt{6}}}\right)$](s3_235.gif)
![$\displaystyle {\textstyle{1\over 6}}\pi a^3\left[{{1\over 4}+\left({{1\over 4}+...
... 6}-{1\over\sqrt{6}}}\right)}\right]
\left({{1\over 2}-{1\over\sqrt{6}}}\right)$](s3_236.gif)