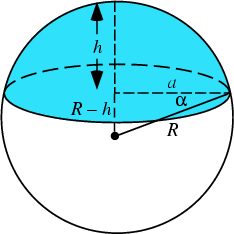
A spherical cap is the region of a Sphere which lies above (or below) a given Plane. If the Plane passes
through the Center of the Sphere, the cap is a Hemisphere. Let the Sphere have Radius 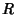 ,
then the Volume of a spherical cap of height
,
then the Volume of a spherical cap of height 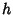 and base Radius
and base Radius 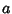 is given by the equation of a
Spherical Segment (which is a spherical cut by a second Plane)
is given by the equation of a
Spherical Segment (which is a spherical cut by a second Plane)
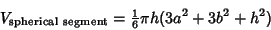 |
(1) |
with 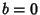 , giving
, giving
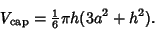 |
(2) |
Using the Pythagorean Theorem gives
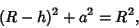 |
(3) |
which can be solved for 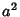 as
as
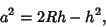 |
(4) |
and plugging this in gives the equivalent formula
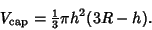 |
(5) |
In terms of the so-called Contact Angle (the angle between the normal to the sphere at the bottom of the cap and the
base plane)
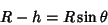 |
(6) |
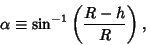 |
(7) |
so
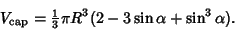 |
(8) |
Consider a cylindrical box enclosing the cap so that the top of the box is tangent to the top of the Sphere. Then the
enclosing box has Volume
so the hollow volume between the cap and box is given by
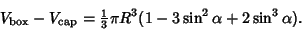 |
(10) |
If a second Plane cuts the cap, the resulting Spherical Frustum is called a Spherical Segment.
The Surface Area of the spherical cap is given by the same equation as for a general Zone:
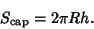 |
(11) |
See also Contact Angle, Dome, Frustum, Hemisphere, Solid of Revolution, Sphere,
Spherical Segment, Torispherical Dome, Zone
© 1996-9 Eric W. Weisstein
1999-05-26
![]() ,
then the Volume of a spherical cap of height
,
then the Volume of a spherical cap of height ![]() and base Radius
and base Radius ![]() is given by the equation of a
Spherical Segment (which is a spherical cut by a second Plane)
is given by the equation of a
Spherical Segment (which is a spherical cut by a second Plane)