|
|
|
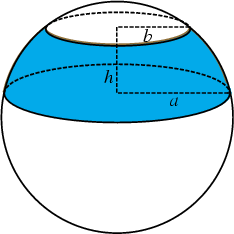
The Surface Area of a Spherical Segment. Call the Radius of the Sphere ![]() , the upper and lower
Radii
, the upper and lower
Radii ![]() and
and ![]() , respectively, and the height of the Spherical Segment
, respectively, and the height of the Spherical Segment ![]() . The zone is a
Surface of Revolution about the z-Axis, so the Surface Area is given by
. The zone is a
Surface of Revolution about the z-Axis, so the Surface Area is given by
| (1) |
| (2) |
| (3) | |||
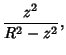 |
(4) |
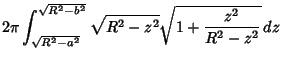 |
|||
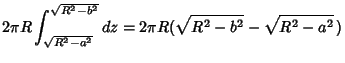 |
|||
| (5) |
See also Sphere, Spherical Cap, Spherical Segment, Zonohedron
References
Beyer, W. H. (Ed.). CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press,
p. 130, 1987.