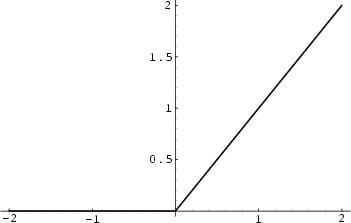
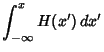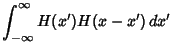where  is the Heaviside Step Function and
is the Heaviside Step Function and 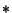 is the Convolution. The Derivative is
is the Convolution. The Derivative is
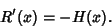 |
(5) |
The Fourier Transform of the ramp function is given by
![\begin{displaymath}
{\mathcal F}[R(x)]=\int_{-\infty}^\infty e^{-2\pi ikx}R(x)\,dx = \pi i\delta'(2\pi k)-{1\over 4\pi^2 k^2},
\end{displaymath}](r_474.gif) |
(6) |
where 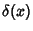 is the Delta Function and
is the Delta Function and 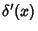 its Derivative.
its Derivative.
See also Fourier Transform--Ramp Function, Heaviside Step Function,
Rectangle Function, Sgn, Square Wave
© 1996-9 Eric W. Weisstein
1999-05-25