|
|
|
The rectangle function ![]() is a function which is 0 outside the interval
is a function which is 0 outside the interval ![]() and unity inside it. It is also called
the Gate Function, Pulse Function, or Window Function, and is defined by
and unity inside it. It is also called
the Gate Function, Pulse Function, or Window Function, and is defined by
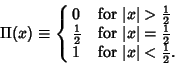 |
(1) |
| (2) | |||
| (3) | |||
| (4) | |||
| (5) |
| (6) |
See also Fourier Transform--Rectangle Function, Heaviside Step Function, Ramp Function