|
|
|
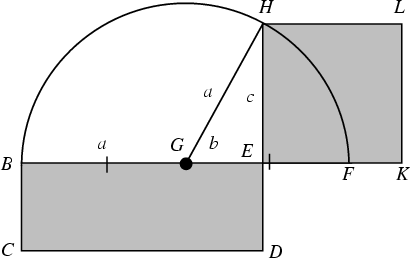
Given a Rectangle
![]() , draw
, draw ![]() on an extension of
on an extension of ![]() . Bisect
. Bisect ![]() and call the Midpoint
and call the Midpoint
![]() . Now draw a Semicircle centered at
. Now draw a Semicircle centered at ![]() , and construct the extension of
, and construct the extension of ![]() which passes through the
Semicircle at
which passes through the
Semicircle at ![]() . Then
. Then
![]() has the same Area as
has the same Area as
![]() . This can be shown as follows:
. This can be shown as follows:
References
Dunham, W. ``Hippocrates' Quadrature of the Lune.'' Ch. 1 in
Journey Through Genius: The Great Theorems of Mathematics.
New York: Wiley, pp. 13-14, 1990.