|
|
|
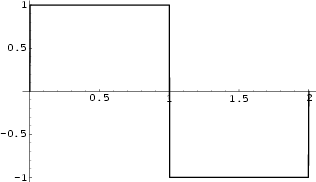
The square wave is a periodic waveform consisting of instantaneous transitions between two levels which can be denoted ![]() .
The square wave is sometimes also called the Rademacher Function. Let the square wave have period
.
The square wave is sometimes also called the Rademacher Function. Let the square wave have period ![]() . The square
wave function is Odd, so the Fourier Series has
. The square
wave function is Odd, so the Fourier Series has ![]() and
and
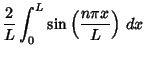 |
|||
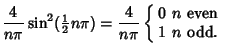 |
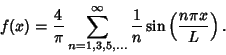
See also Hadamard Matrix, Walsh Function
References
Thompson, A. R.; Moran, J. M.; and Swenson, G. W. Jr. Interferometry and Synthesis in Radio Astronomy. New York:
Wiley, p. 203, 1986.