|
|
|
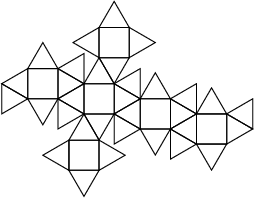
|
An Archimedean Solid also called the Snub Cuboctahedron whose Vertices are the 24
points on the surface of a Sphere for which the smallest distance between any two is as great as possible. It has two
Enantiomers, and its Dual Polyhedron is the Pentagonal Icositetrahedron. It has
Schläfli Symbol s
![]() . It is also Uniform Polyhedron
. It is also Uniform Polyhedron ![]() and
has Wythoff Symbol
and
has Wythoff Symbol ![]() . Its faces are
. Its faces are
![]() .
.
The Inradius, Midradius, and Circumradius for ![]() are
are
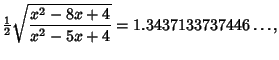 |
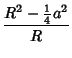 |
|||
See also Snub Dodecahedron
References
Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, p. 139, 1987.
Coxeter, H. S. M.; Longuet-Higgins, M. S.; and Miller, J. C. P. ``Uniform Polyhedra.''
Phil. Trans. Roy. Soc. London Ser. A 246, 401-450, 1954.