|
|
|
Given a differential equation
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
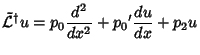 |
(6) | ||
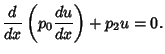 |
(7) |
A nonself-adjoint second-order linear differential operator can always be transformed into a self-adjoint one using
Sturm-Liouville Theory. In the special case ![]() , (7) gives
, (7) gives
| (8) |
| (9) |
| (10) |
| (11) |
A self-adjoint operator which satisfies the Boundary Conditions
| (12) |
See also Adjoint Operator, Hermitian Operator, Sturm-Liouville Theory
References
Arfken, G. ``Self-Adjoint Differential Equations.'' §9.1 in Mathematical Methods for Physicists, 3rd ed.
Orlando, FL: Academic Press, pp. 497-509, 1985.
|
|
|
© 1996-9 Eric W. Weisstein