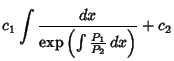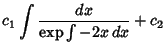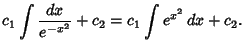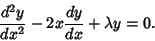 |
(1) |
This differential equation has an irregular singularity at 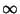 . It can be solved using the series method
. It can be solved using the series method
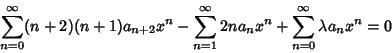 |
(2) |
![\begin{displaymath}
(2a_2+\lambda a_4) + \sum_{n=1}^\infty [(n+2)(n+1)a_{n+2}-2na_n+\lambda a_n]x^n = 0.
\end{displaymath}](h_1329.gif) |
(3) |
Therefore,
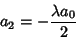 |
(4) |
and
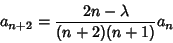 |
(5) |
for 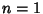 , 2, .... Since (4) is just a special case of (5),
, 2, .... Since (4) is just a special case of (5),
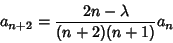 |
(6) |
for 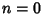 , 1, .... The linearly independent solutions are then
, 1, .... The linearly independent solutions are then
If
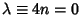 , 4, 8, ..., then
, 4, 8, ..., then 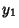 terminates with the Power
terminates with the Power 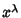 , and
, and 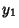 (normalized so that
the Coefficient of
(normalized so that
the Coefficient of 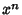 is
is 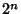 ) is the regular solution to the equation, known as the Hermite Polynomial. If
) is the regular solution to the equation, known as the Hermite Polynomial. If
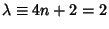 , 6, 10, ..., then
, 6, 10, ..., then 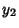 terminates with the Power
terminates with the Power 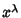 , and
, and 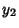 (normalized so
that the Coefficient of
(normalized so
that the Coefficient of 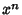 is
is 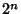 ) is the regular solution to the equation, known as the Hermite Polynomial.
) is the regular solution to the equation, known as the Hermite Polynomial.
If 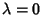 , then Hermite's differential equation becomes
, then Hermite's differential equation becomes
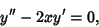 |
(9) |
which is of the form
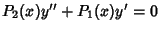 and so has solution
and so has solution
© 1996-9 Eric W. Weisstein
1999-05-25
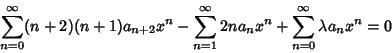
![\begin{displaymath}
(2a_2+\lambda a_4) + \sum_{n=1}^\infty [(n+2)(n+1)a_{n+2}-2na_n+\lambda a_n]x^n = 0.
\end{displaymath}](h_1329.gif)
![$\displaystyle a_0\left[{1 - {\lambda\over 2!} \,x^2 - {(4-\lambda )\lambda\over 4!}\, x^4 - {(8-\lambda)(4-\lambda)\lambda\over 6!} \,x^6 - \ldots}\right]$](h_1334.gif)
![$\displaystyle a_1\left[{x + {(2-\lambda)\over 3!} \,x^3 + {(6-\lambda)(2-\lambda)\over 5!}\, x^5 + \ldots}\right].$](h_1336.gif)
![]() , then Hermite's differential equation becomes
, then Hermite's differential equation becomes