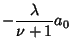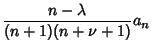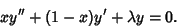 |
(1) |
The Laguerre differential equation is a special case of the more general ``associated Laguerre differential equation''
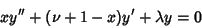 |
(2) |
with 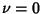 . Note that if
. Note that if 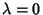 , then the solution to the associated Laguerre differential equation is of the
form
, then the solution to the associated Laguerre differential equation is of the
form
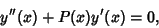 |
(3) |
and the solution can be found using an Integrating Factor
so
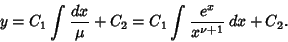 |
(5) |
The associated Laguerre differential equation has a Regular Singular Point at 0 and an Irregular
Singularity at 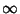 . It can be solved using a series expansion,
. It can be solved using a series expansion,
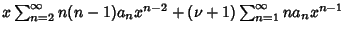
|
|
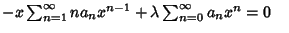
|
(6) |
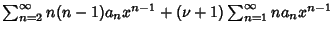
|
|
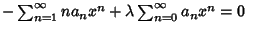
|
(7) |
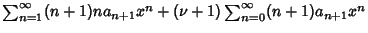
|
|
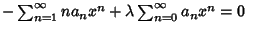
|
(8) |
![\begin{displaymath}[(n+1)a_1+\lambda a_0]+ \sum_{n=1}^\infty \{[(n+1)n+(\nu+1)(n+1)]a_{n+1}-na_n+\lambda a_n\}x^n = 0
\end{displaymath}](l1_189.gif) |
(9) |
![\begin{displaymath}[(n+1)a_1+\lambda a_0]+ \sum_{n=1}^\infty [(n+1)(n+\nu+1)a_{n+1}+(\lambda-n)a_n]x^n = 0.
\end{displaymath}](l1_190.gif) |
(10) |
This requires
for 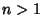 . Therefore,
. Therefore,
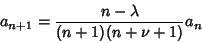 |
(13) |
for 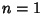 , 2, ..., so
, 2, ..., so
![\begin{displaymath}
y=a_0\left[{1-{\lambda \over \nu+1}x-{\lambda (1-\lambda )\o...
...-\lambda )\over 2\cdot 3(\nu+1)(\nu+2)(\nu+3)}+\cdots}\right].
\end{displaymath}](l1_198.gif) |
(14) |
If 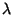 is a Positive Integer, then the series terminates and the solution is a Polynomial, known
as an associated Laguerre Polynomial (or, if
is a Positive Integer, then the series terminates and the solution is a Polynomial, known
as an associated Laguerre Polynomial (or, if 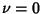 , simply a
Laguerre Polynomial).
, simply a
Laguerre Polynomial).
See also Laguerre Polynomial
© 1996-9 Eric W. Weisstein
1999-05-26
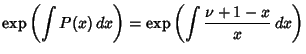
![]() . It can be solved using a series expansion,
. It can be solved using a series expansion,
![\begin{displaymath}[(n+1)a_1+\lambda a_0]+ \sum_{n=1}^\infty \{[(n+1)n+(\nu+1)(n+1)]a_{n+1}-na_n+\lambda a_n\}x^n = 0
\end{displaymath}](l1_189.gif)
![\begin{displaymath}[(n+1)a_1+\lambda a_0]+ \sum_{n=1}^\infty [(n+1)(n+\nu+1)a_{n+1}+(\lambda-n)a_n]x^n = 0.
\end{displaymath}](l1_190.gif)