Also called Gauss-Laguerre Quadrature or Laguerre Quadrature. A Gaussian Quadrature over
the interval 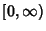 with Weighting Function
with Weighting Function 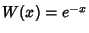 . The Abscissas for quadrature order
. The Abscissas for quadrature order 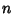 are
given by the Roots of the Laguerre Polynomials
are
given by the Roots of the Laguerre Polynomials 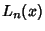 . The weights are
. The weights are
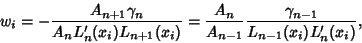 |
(1) |
where 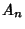 is the Coefficient of
is the Coefficient of 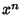 in
in 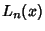 . For Laguerre Polynomials,
. For Laguerre Polynomials,
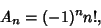 |
(2) |
where 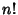 is a Factorial, so
is a Factorial, so
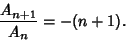 |
(3) |
Additionally,
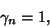 |
(4) |
so
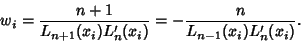 |
(5) |
(Note that the normalization used here is different than that in Hildebrand 1956.) Using the recurrence relation
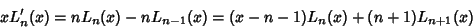 |
(6) |
which implies
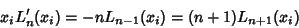 |
(7) |
gives
![\begin{displaymath}
w_i={1\over x_i[L_n'(x_i)]^2}={x_i\over (n+1)^2[L_{n+1}(x_i)]^2}.
\end{displaymath}](l1_212.gif) |
(8) |
The error term is
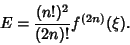 |
(9) |
Beyer (1987) gives a table of Abscissas and weights up to 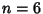 .
.
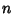 |
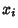 |
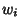 |
| 2 |
0.585786 |
0.853553 |
| |
3.41421 |
0.146447 |
| 3 |
0.415775 |
0.711093 |
| |
2.29428 |
0.278518 |
| |
6.28995 |
0.0103893 |
| 4 |
0.322548 |
0.603154 |
| |
1.74576 |
0.357419 |
| |
4.53662 |
0.0388879 |
| |
9.39507 |
0.000539295 |
| 5 |
0.26356 |
0.521756 |
| |
1.4134 |
0.398667 |
| |
3.59643 |
0.0759424 |
| |
7.08581 |
0.00361176 |
| |
12.6408 |
0.00002337 |
The Abscissas and weights can be computed analytically for small 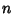 .
.
For the associated Laguerre polynomial 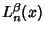 with Weighting Function
with Weighting Function
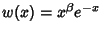 ,
,
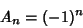 |
(10) |
and
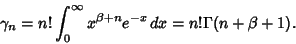 |
(11) |
The weights are
![\begin{displaymath}
w_i={n!\Gamma(n+\beta+1)\over x_i[{L_m^\beta}'(x_i)]^2}={n!\Gamma(n+\beta+1)x_i\over [L_{n+1}^\beta(x_i)]^2},
\end{displaymath}](l1_225.gif) |
(12) |
where 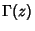 is the Gamma Function, and the error term is
is the Gamma Function, and the error term is
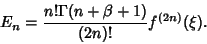 |
(13) |
References
Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 463, 1987.
Chandrasekhar, S. Radiative Transfer. New York: Dover, pp. 64-65, 1960.
Hildebrand, F. B. Introduction to Numerical Analysis. New York: McGraw-Hill, pp. 325-327, 1956.
© 1996-9 Eric W. Weisstein
1999-05-26
![]() with Weighting Function
with Weighting Function ![]() . The Abscissas for quadrature order
. The Abscissas for quadrature order ![]() are
given by the Roots of the Laguerre Polynomials
are
given by the Roots of the Laguerre Polynomials ![]() . The weights are
. The weights are
![]() .
.
![]() .
.
![]() with Weighting Function
with Weighting Function
![]() ,
,