Consider a second-order Ordinary Differential Equation
If 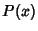 and
and 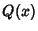 remain Finite at
remain Finite at 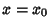 , then
, then 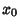 is called an Ordinary Point. If either
is called an Ordinary Point. If either 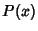 or
or
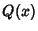 diverges as
diverges as 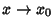 , then
, then 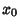 is called a singular point. If
is called a singular point. If 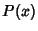 diverges more quickly than
diverges more quickly than 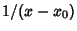 , so
, so
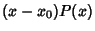 approaches Infinity as
approaches Infinity as 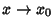 , or
, or 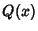 diverges more quickly than
diverges more quickly than 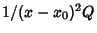 so that
so that
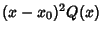 goes to Infinity as
goes to Infinity as 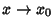 , then
, then 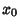 is called an Irregular Singularity (or
Essential Singularity).
is called an Irregular Singularity (or
Essential Singularity).
See also Ordinary Point, Regular Singular Point, Singular Point (Differential Equation)
References
Arfken, G. ``Singular Points.'' §8.4 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press,
pp. 451-453 and 461-463, 1985.
© 1996-9 Eric W. Weisstein
1999-05-26