A Matrix A for which
where the Adjoint Operator is denoted
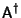 ,
,
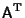 is the Matrix Transpose, and
is the Matrix Transpose, and 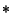 is the
Complex Conjugate. If a Matrix is self-adjoint, it is said to be Hermitian.
is the
Complex Conjugate. If a Matrix is self-adjoint, it is said to be Hermitian.
See also Adjoint Operator, Hermitian Matrix, Matrix Transpose
© 1996-9 Eric W. Weisstein
1999-05-26