If a Matrix is Self-Adjoint, it is said to be a Hermitian matrix. Therefore, a
Hermitian Matrix is defined as one for which
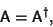 |
(1) |
where 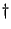 denotes the Adjoint Matrix. Hermitian Matrices have Real
Eigenvalues with Orthogonal Eigenvectors. For
Real Matrices, Hermitian is the same as symmetrical. Any Matrix
denotes the Adjoint Matrix. Hermitian Matrices have Real
Eigenvalues with Orthogonal Eigenvectors. For
Real Matrices, Hermitian is the same as symmetrical. Any Matrix
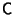 which is not Hermitian can be expressed as the sum of two Hermitian matrices
which is not Hermitian can be expressed as the sum of two Hermitian matrices
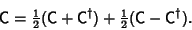 |
(2) |
Let
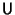 be a Unitary Matrix and
be a Unitary Matrix and
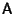 be a Hermitian matrix. Then the Adjoint Matrix of a
Similarity Transformation is
be a Hermitian matrix. Then the Adjoint Matrix of a
Similarity Transformation is
The specific matrix
![\begin{displaymath}
{\hbox{\sf H}}(x,y,z)=\left[{\matrix{z & x+iy\cr x-iy & -z}}\right] = x{\hbox{\sf P}}_1+y{\hbox{\sf P}}_2+z{\hbox{\sf P}}_3,
\end{displaymath}](h_1479.gif) |
(4) |
where
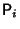 are Pauli Spin Matrices, is sometimes called ``the'' Hermitian matrix.
are Pauli Spin Matrices, is sometimes called ``the'' Hermitian matrix.
See also Adjoint Matrix, Hermitian Operator, Pauli Spin Matrices
References
Arfken, G. ``Hermitian Matrices, Unitary Matrices.'' §4.5 in Mathematical Methods for Physicists, 3rd ed.
Orlando, FL: Academic Press, pp. 209-217, 1985.
© 1996-9 Eric W. Weisstein
1999-05-25