The procedure of finding the value of one or more parameters for a given statistic which makes the known
Likelihood distribution a Maximum. The maximum likelihood estimate for a parameter 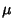 is denoted
is denoted
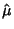 .
.
For a Bernoulli Distribution,
![\begin{displaymath}
{d\over d\theta} \left[{{N\choose Np} \theta^{Np}(1-\theta )^{Nq}}\right]= Np(1-\theta)-\theta Nq = 0,
\end{displaymath}](m_716.gif) |
(1) |
so maximum likelihood occurs for 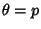 . If
. If 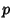 is not known ahead of time, the likelihood function is
is not known ahead of time, the likelihood function is
where 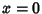 or 1, and
or 1, and 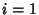 , ...,
, ..., 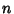 .
.
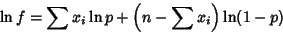 |
(3) |
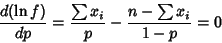 |
(4) |
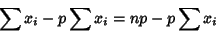 |
(5) |
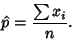 |
(6) |
For a Gaussian Distribution,
![\begin{displaymath}
f(x_1,\ldots,x_n\vert\mu,\sigma) = \prod {1\over\sigma\sqrt{...
...xp}\nolimits \left[{-{\sum (x_i-\mu)^2\over 2\sigma^2}}\right]
\end{displaymath}](m_728.gif) |
(7) |
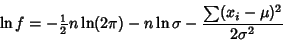 |
(8) |
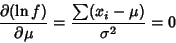 |
(9) |
gives
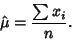 |
(10) |
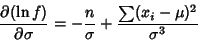 |
(11) |
gives
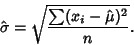 |
(12) |
Note that in this case, the maximum likelihood Standard Deviation is the sample Standard Deviation, which
is a Biased Estimator for the population Standard Deviation.
For a weighted Gaussian Distribution,
![\begin{displaymath}
f(x_1,\ldots,x_n\vert\mu,\sigma) = \prod {1\over\sigma_i\sqr...
...xp}\nolimits \left[{-{\sum (x_i-\mu)^2\over 2\sigma^2}}\right]
\end{displaymath}](m_734.gif) |
(13) |
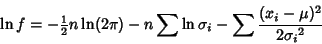 |
(14) |
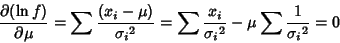 |
(15) |
gives
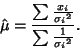 |
(16) |
The Variance of the Mean is then
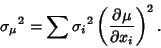 |
(17) |
But
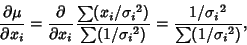 |
(18) |
so
For a Poisson Distribution,
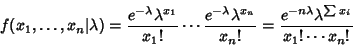 |
(20) |
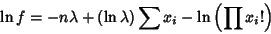 |
(21) |
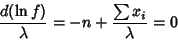 |
(22) |
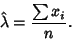 |
(23) |
See also Bayesian Analysis
References
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. ``Least Squares as a Maximum Likelihood
Estimator.'' §15.1 in
Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England:
Cambridge University Press, pp. 651-655, 1992.
© 1996-9 Eric W. Weisstein
1999-05-26
![]() is denoted
is denoted
![]() .
.
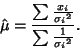
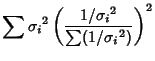
![$\displaystyle \sum {1/{\sigma_i}^2\over \left[{\sum (1/{\sigma_i}^2)}\right]^2} = {1\over\sum (1/{\sigma_i}^2)}.$](m_742.gif)