|
|
|
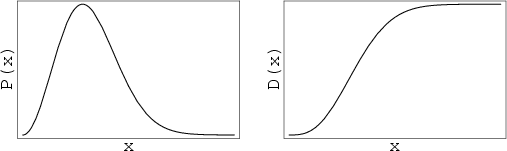
The distribution of speeds of molecules in thermal equilibrium as given by
statistical mechanics. ![]() The probability and cumulative distributions are
The probability and cumulative distributions are
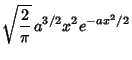 |
(1) | ||
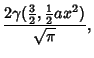 |
(2) |
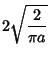 |
(3) | ||
| (4) | |||
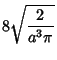 |
(5) | ||
| (6) |
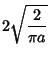 |
(7) | ||
| (8) | |||
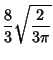 |
(9) | ||
| (10) |
See also Exponential Distribution, Gaussian Distribution, Rayleigh Distribution
References
Spiegel, M. R. Theory and Problems of Probability and Statistics. New York: McGraw-Hill, p. 119, 1992.
von Seggern, D. CRC Standard Curves and Surfaces. Boca Raton, FL: CRC Press, p. 252, 1993.