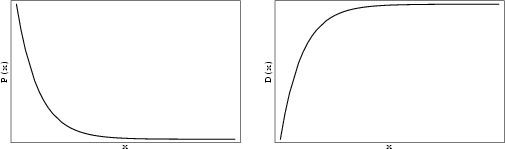
Given a Poisson Distribution with rate of change 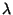 , the distribution of waiting times between successive
changes (with
, the distribution of waiting times between successive
changes (with 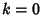 ) is
) is
which is normalized since
This is the only Memoryless Random Distribution. Define the Mean
waiting time between successive changes as
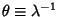 . Then
. Then
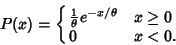 |
(4) |
The Moment-Generating Function is
so
The Skewness and Kurtosis are given by
The Mean and Variance can also be computed directly
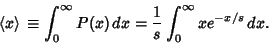 |
(15) |
Use the integral
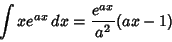 |
(16) |
to obtain
Now, to find
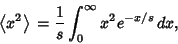 |
(18) |
use the integral
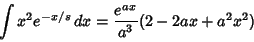 |
(19) |
giving
If a generalized exponential probability function is defined by
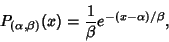 |
(23) |
then the Characteristic Function is
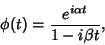 |
(24) |
and the Mean, Variance, Skewness, and Kurtosis are
See also Double Exponential Distribution
References
Balakrishnan, N. and Basu, A. P. The Exponential Distribution: Theory, Methods, and Applications.
New York: Gordon and Breach, 1996.
Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, pp. 534-535, 1987.
Spiegel, M. R. Theory and Problems of Probability and Statistics. New York: McGraw-Hill, p. 119, 1992.
© 1996-9 Eric W. Weisstein
1999-05-25
![]() , the distribution of waiting times between successive
changes (with
, the distribution of waiting times between successive
changes (with ![]() ) is
) is
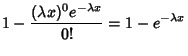
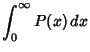
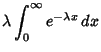
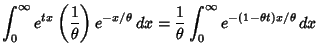
![$\displaystyle \left[{e^{-(1-\theta t)x/\theta} \over 1-\theta t}\right]_0^\infty = {1\over 1-\theta t}$](e_2682.gif)
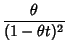
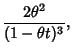
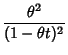
![$\displaystyle {1\over s}\left[{{e^{-x/s}\over\left({-{1\over s}}\right)^2} \left\{{\left({-{1\over s}}\right)x-1}\right\}}\right]^\infty_0$](e_2700.gif)
![$\displaystyle {1\over s}\left[{{e^{-x/s}\over\left({-{1\over s}}\right)^3} \left({2+{2\over s} x+{1\over s^2} x^2}\right)}\right]_0^\infty$](e_2706.gif)