A mathematical procedure for finding the best fitting curve to a given set of points by minimizing the sum of the squares of the
offsets (``the residuals'') of the points from the curve. The sum of the squares of the offsets is used instead of the
offset absolute values because this allows the residuals to be treated as a continuous differentiable quantity. However, because
squares of the offsets are used, outlying points can have a disproportionate effect on the fit, a property which may or may not
be desirable depending on the problem at hand.
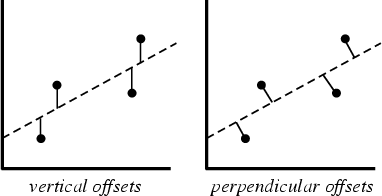
In practice, the vertical offsets from a line are almost always minimized instead of the perpendicular offsets. This
allows uncertainties of the data points along the 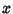 - and
- and 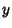 -axes to be incorporated simply, and also provides a much simpler
analytic form for the fitting parameters than would be obtained using a fit based on perpendicular distances. In addition, the
fitting technique can be easily generalized from a best-fit line to a best-fit polynomial when sums of vertical
distances are used (which is not the case using perpendicular distances). For a reasonable number of noisy data points, the
difference between vertical and perpendicular fits is quite small.
-axes to be incorporated simply, and also provides a much simpler
analytic form for the fitting parameters than would be obtained using a fit based on perpendicular distances. In addition, the
fitting technique can be easily generalized from a best-fit line to a best-fit polynomial when sums of vertical
distances are used (which is not the case using perpendicular distances). For a reasonable number of noisy data points, the
difference between vertical and perpendicular fits is quite small.
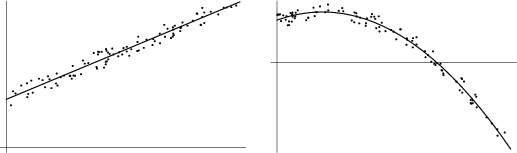
The linear least squares fitting technique is the simplest and most commonly applied form of Linear Regression and
provides a solution to the problem of finding the best fitting straight line through a set of points. In fact, if the
functional relationship between the two quantities being graphed is known to within additive or multiplicative constants, it is
common practice to transform the data in such a way that the resulting line is a straight line, say by plotting 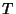 vs.
vs. 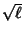 instead of
instead of 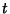 vs.
vs. 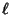 . For this reason, standard forms for Exponential, Logarithmic, and Power
laws are often explicitly computed. The formulas for linear least squares fitting were independently derived by Gauß
. For this reason, standard forms for Exponential, Logarithmic, and Power
laws are often explicitly computed. The formulas for linear least squares fitting were independently derived by Gauß  and
Legendre.
and
Legendre. 
For Nonlinear Least Squares Fitting to a number of unknown parameters, linear least squares fitting may be applied
iteratively to a linearized form of the function until convergence is achieved. Depending on the type of fit and initial
parameters chosen, the nonlinear fit may have good or poor convergence properties. If uncertainties (in the most general case,
error ellipses) are given for the points, points can be weighted differently in order to give the high-quality points more
weight.
The residuals of the best-fit line for a set of 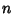 points using unsquared perpendicular distances
points using unsquared perpendicular distances 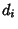 of points
of points 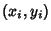 are given by
are given by
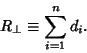 |
(1) |
Since the perpendicular distance from a line 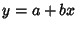 to point
to point 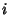 is given by
is given by
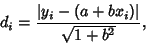 |
(2) |
the function to be minimized is
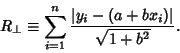 |
(3) |
Unfortunately, because the absolute value function does not have continuous derivatives, minimizing 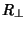 is not
amenable to analytic solution. However, if the square of the perpendicular distances
is not
amenable to analytic solution. However, if the square of the perpendicular distances
![\begin{displaymath}
R_\perp^2\equiv \sum_{i=1}^n {[y_i-(a+bx_i)]^2\over 1+b^2}
\end{displaymath}](l1_1039.gif) |
(4) |
is minimized instead, the problem can be solved in closed form. 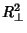 is a minimum when (suppressing the indices)
is a minimum when (suppressing the indices)
=0
\end{displaymath}](l1_1041.gif) |
(5) |
and
 +\sum {[y-(a+bx)]^2(-1)(2b)\over (1+b^2)^2} = 0.
\end{displaymath}](l1_1042.gif) |
(6) |
The former gives
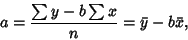 |
(7) |
and the latter
![\begin{displaymath}
(1+b^2)\sum [y-(a+bx)]x+b\sum [y-(a+bx)]^2=0.
\end{displaymath}](l1_1044.gif) |
(8) |
But
![\begin{displaymath}[y-(a+bx)]^2 =y^2-2(a+bx)y+(a+bx)^2 = y^2-2ay-2bxy+a^2+2abx+b^2x^2,
\end{displaymath}](l1_1045.gif) |
(9) |
so (8) becomes
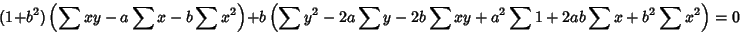 |
(10) |
![$[(1+b^2)(-b)+b(b^2)]\sum x^2+[(1+b^2)-2b^2]\sum xy$](l1_1047.gif)
|
|
![$ +b\sum y^2+[-a(1+b^2)+2ab^2]\sum x-2ab\sum y+ba^2\sum 1=0$](l1_1048.gif)
|
(11) |
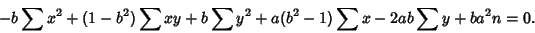 |
(12) |
Plugging (7) into (12) then gives
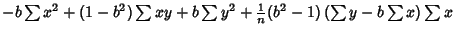
|
|
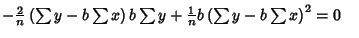
|
(13) |
After a fair bit of algebra, the result is
![\begin{displaymath}
b^2+{\sum y^2-\sum x^2+{1\over n}\left[{\left({\sum x}\right...
...}\right)^2}\right]\over {1\over n}\sum x\sum y-\sum xy} b-1=0.
\end{displaymath}](l1_1052.gif) |
(14) |
So define
and the Quadratic Formula gives
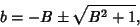 |
(16) |
with 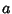 found using (7). Note the rather unwieldy form of the best-fit parameters in the formulation. In addition,
minimizing
found using (7). Note the rather unwieldy form of the best-fit parameters in the formulation. In addition,
minimizing 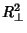 for a second- or higher-order Polynomial leads to polynomial equations having higher order,
so this formulation cannot be extended.
for a second- or higher-order Polynomial leads to polynomial equations having higher order,
so this formulation cannot be extended.
Vertical least squares fitting proceeds by finding the sum of the squares of the vertical deviations 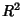 of a set
of
of a set
of 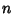 data points
data points
![\begin{displaymath}
R^2 \equiv \sum[y_i-f(x_i, a_1, a_2, \ldots, a_n)]^2
\end{displaymath}](l1_1058.gif) |
(17) |
from a function 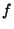 . Note that this procedure does not minimize the actual deviations from the line (which would be
measured perpendicular to the given function). In addition, although the unsquared sum of distances might seem a more
appropriate quantity to minimize, use of the absolute value results in discontinuous derivatives which cannot be treated
analytically. The square deviations from each point are therefore summed, and the resulting residual is then minimized to
find the best fit line. This procedure results in outlying points being given disproportionately large weighting.
. Note that this procedure does not minimize the actual deviations from the line (which would be
measured perpendicular to the given function). In addition, although the unsquared sum of distances might seem a more
appropriate quantity to minimize, use of the absolute value results in discontinuous derivatives which cannot be treated
analytically. The square deviations from each point are therefore summed, and the resulting residual is then minimized to
find the best fit line. This procedure results in outlying points being given disproportionately large weighting.
The condition for 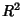 to be a minimum is that
to be a minimum is that
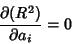 |
(18) |
for 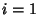 , ...,
, ..., 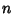 . For a linear fit,
. For a linear fit,
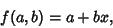 |
(19) |
so
![\begin{displaymath}
R^2(a,b) \equiv \sum_{i=1}^n [y_i-(a+bx_i)]^2
\end{displaymath}](l1_1062.gif) |
(20) |
![\begin{displaymath}
{\partial (R^2)\over\partial a} = -2\sum_{i=1}^n [y_i-(a+bx_i)] = 0
\end{displaymath}](l1_1063.gif) |
(21) |
![\begin{displaymath}
{\partial (R^2)\over\partial b} = -2\sum_{i=1}^n [y_i-(a+bx_i)]x_i = 0.
\end{displaymath}](l1_1064.gif) |
(22) |
These lead to the equations
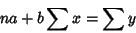 |
(23) |
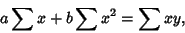 |
(24) |
where the subscripts have been dropped for conciseness. In Matrix form,
![\begin{displaymath}
\left[{\matrix{n & \sum x\cr \sum x& \sum x^2\cr}}\right]\le...
...r b\cr}}\right]= \left[{\matrix{\sum y\cr \sum xy\cr}}\right],
\end{displaymath}](l1_1067.gif) |
(25) |
so
![\begin{displaymath}
\left[{\matrix{a\cr b\cr}}\right] =\left[{\matrix{n & \sum x...
...\cr}}\right]^{-1}\left[{\matrix{\sum y\cr \sum xy\cr}}\right].
\end{displaymath}](l1_1068.gif) |
(26) |
The  Matrix Inverse is
Matrix Inverse is
![\begin{displaymath}
\left[{\matrix{a\cr b\cr}}\right] = {1\over n\sum x^2-\left(...
... y\sum x^2-\sum x\sum xy\cr n\sum xy-\sum x\sum y\cr}}\right],
\end{displaymath}](l1_1070.gif) |
(27) |
so
(Kenney and Keeping 1962). These can be rewritten in a simpler form by defining the sums of squares
which are also written as
Here,
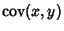 is the Covariance and
is the Covariance and 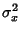 and
and 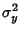 are variances. Note that the quantities
are variances. Note that the quantities 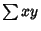 and
and 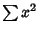 can also be interpreted as the Dot Products
can also be interpreted as the Dot Products
In terms of the sums of squares, the Regression Coefficient 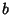 is given by
is given by
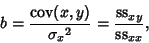 |
(40) |
and 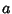 is given in terms of
is given in terms of 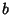 using (24) as
using (24) as
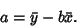 |
(41) |
The overall quality of the fit is then parameterized in terms of a quantity known as the Correlation Coefficient,
defined by
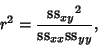 |
(42) |
which gives the proportion of 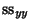 which is accounted for by the regression.
which is accounted for by the regression.
The Standard Errors for 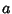 and
and 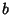 are
are
Let 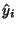 be the vertical coordinate of the best-fit line with
be the vertical coordinate of the best-fit line with 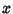 -coordinate
-coordinate 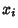 , so
, so
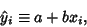 |
(45) |
then the error between the actual vertical point 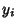 and the fitted point is given by
and the fitted point is given by
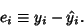 |
(46) |
Now define 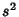 as an estimator for the variance in
as an estimator for the variance in 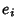 ,
,
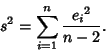 |
(47) |
Then 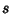 can be given by
can be given by
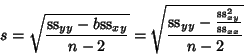 |
(48) |
(Acton 1966, pp. 32-35; Gonick and Smith 1993, pp. 202-204).
Generalizing from a straight line (i.e., first degree polynomial) to a 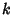 th degree Polynomial
th degree Polynomial
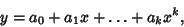 |
(49) |
the residual is given by
![\begin{displaymath}
R^2 \equiv \sum_{i=1}^n [y_i-(a_0+a_1x_i+\ldots +a_k{x_i}^k)]^2.
\end{displaymath}](l1_1113.gif) |
(50) |
The Partial Derivatives (again dropping superscripts) are
![\begin{displaymath}
{\partial(R^2)\over\partial a_0} = -2 \sum [y-(a_0+a_1x+\ldots +a_kx^k)] = 0
\end{displaymath}](l1_1114.gif) |
(51) |
![\begin{displaymath}
{\partial(R^2)\over\partial a_1} = -2 \sum [y-(a_0+a_1x+\ldots +a_kx^k)]x = 0
\end{displaymath}](l1_1115.gif) |
(52) |
![\begin{displaymath}
{\partial(R^2)\over\partial a_k} = -2 \sum [y-(a_0+a_1x+\ldots +a_kx^k)]x^k = 0.
\end{displaymath}](l1_1116.gif) |
(53) |
These lead to the equations
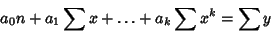 |
(54) |
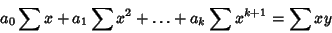 |
(55) |
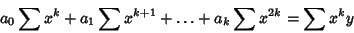 |
(56) |
or, in Matrix form
![$\left[{\matrix{n & \sum x& \cdots & \sum x^k\cr \sum x& \sum x^2& \cdots & \sum...
...right] = \left[{\matrix{\sum y\cr \sum xy\cr \vdots\cr \sum x^ky\cr}}\right]\!.$](l1_1120.gif)
|
|
|
|
(57) |
This is a Vandermonde Matrix. We can also obtain the Matrix for a least squares fit by writing
![\begin{displaymath}
\left[{\matrix{1 & x_1 & \cdots & {x_1}^k\cr
1 & x_2 & \cdo...
...ght] = \left[{\matrix{y_1\cr y_2\cr \vdots\cr y_n\cr}}\right].
\end{displaymath}](l1_1121.gif) |
(58) |
Premultiplying both sides by the Transpose of the first Matrix then gives
![\begin{displaymath}
\left[{\matrix{1 & 1 & \cdots & 1\cr x_1 & x_2 & \cdots & x_...
...right] \left[{\matrix{y_1\cr y_2\cr \vdots\cr y_n\cr}}\right],
\end{displaymath}](l1_1122.gif) |
(59) |
so
![\begin{displaymath}
\left[{\matrix{n & \sum x& \cdots & \sum x^n\cr \sum x& \sum...
...{\matrix{\sum y\cr \sum xy\cr \vdots\cr \sum x^ky\cr}}\right].
\end{displaymath}](l1_1123.gif) |
(60) |
As before, given 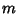 points
points 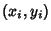 and fitting with Polynomial Coefficients
and fitting with Polynomial Coefficients 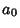 ,
...,
,
..., 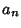 gives
gives
![\begin{displaymath}
\left[{\matrix{y_1\cr y_2\cr \vdots\cr y_m\cr}}\right] = \le...
...right] \left[{\matrix{a_0\cr a_1\cr \vdots\cr a_n\cr}}\right],
\end{displaymath}](l1_1125.gif) |
(61) |
In Matrix notation, the equation for a polynomial fit is given by
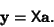 |
(62) |
This can be solved by premultiplying by the Matrix Transpose
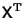 ,
,
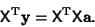 |
(63) |
This Matrix Equation can be solved numerically, or can be inverted directly if it is well formed, to yield the
solution vector
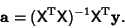 |
(64) |
Setting 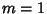 in the above equations reproduces the linear solution.
in the above equations reproduces the linear solution.
See also Correlation Coefficient, Interpolation, Least Squares Fitting--Exponential, Least Squares Fitting--Logarithmic, Least
Squares Fitting--Power Law, Moore-Penrose Generalized Matrix Inverse,
Nonlinear Least Squares Fitting, Regression Coefficient, Spline
References
Acton, F. S. Analysis of Straight-Line Data. New York: Dover, 1966.
Bevington, P. R. Data Reduction and Error Analysis for the Physical Sciences. New York: McGraw-Hill, 1969.
Gonick, L. and Smith, W. The Cartoon Guide to Statistics. New York: Harper Perennial, 1993.
Kenney, J. F. and Keeping, E. S. ``Linear Regression, Simple Correlation, and Contingency.'' Ch. 8 in
Mathematics of Statistics, Pt. 2, 2nd ed. Princeton, NJ: Van Nostrand, pp. 199-237, 1951.
Kenney, J. F. and Keeping, E. S. ``Linear Regression and Correlation.'' Ch. 15 in Mathematics of Statistics, Pt. 1, 3rd ed.
Princeton, NJ: Van Nostrand, pp. 252-285, 1962.
Lancaster, P. and Salkauskas, K. Curve and Surface Fitting: An Introduction. London: Academic Press, 1986.
Lawson, C. and Hanson, R. Solving Least Squares Problems. Englewood Cliffs, NJ: Prentice-Hall, 1974.
Nash, J. C. Compact Numerical Methods for Computers: Linear Algebra
and Function Minimisation, 2nd ed. Bristol, England: Adam Hilger, pp. 21-24, 1990.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. ``Fitting Data to a Straight Line''
``Straight-Line Data with Errors in Both Coordinates,'' and ``General Linear Least Squares.'' §15.2, 15.3, and 15.4 in
Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England:
Cambridge University Press, pp. 655-675, 1992.
York, D. ``Least-Square Fitting of a Straight Line.'' Canad. J. Phys. 44, 1079-1086, 1966.
© 1996-9 Eric W. Weisstein
1999-05-26

![]() - and
- and ![]() -axes to be incorporated simply, and also provides a much simpler
analytic form for the fitting parameters than would be obtained using a fit based on perpendicular distances. In addition, the
fitting technique can be easily generalized from a best-fit line to a best-fit polynomial when sums of vertical
distances are used (which is not the case using perpendicular distances). For a reasonable number of noisy data points, the
difference between vertical and perpendicular fits is quite small.
-axes to be incorporated simply, and also provides a much simpler
analytic form for the fitting parameters than would be obtained using a fit based on perpendicular distances. In addition, the
fitting technique can be easily generalized from a best-fit line to a best-fit polynomial when sums of vertical
distances are used (which is not the case using perpendicular distances). For a reasonable number of noisy data points, the
difference between vertical and perpendicular fits is quite small.
![]() vs.
vs. ![]() instead of
instead of ![]() vs.
vs. ![]() . For this reason, standard forms for Exponential, Logarithmic, and Power
laws are often explicitly computed. The formulas for linear least squares fitting were independently derived by Gauß
. For this reason, standard forms for Exponential, Logarithmic, and Power
laws are often explicitly computed. The formulas for linear least squares fitting were independently derived by Gauß ![]() and
Legendre.
and
Legendre. ![]()
![]() points using unsquared perpendicular distances
points using unsquared perpendicular distances ![]() of points
of points ![]() are given by
are given by
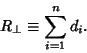
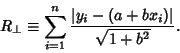
![]() is not
amenable to analytic solution. However, if the square of the perpendicular distances
is not
amenable to analytic solution. However, if the square of the perpendicular distances
![\begin{displaymath}
R_\perp^2\equiv \sum_{i=1}^n {[y_i-(a+bx_i)]^2\over 1+b^2}
\end{displaymath}](l1_1039.gif)
![\begin{displaymath}
b^2+{\sum y^2-\sum x^2+{1\over n}\left[{\left({\sum x}\right...
...}\right)^2}\right]\over {1\over n}\sum x\sum y-\sum xy} b-1=0.
\end{displaymath}](l1_1052.gif)
![$\displaystyle {1\over 2}{\left[{\sum y^2-{1\over n}\left({\sum y}\right)^2}\rig...
...-{1\over n}\left({\sum x}\right)^2}\right]\over {1\over n}\sum x\sum y-\sum xy}$](l1_1054.gif)
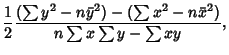
![]() of a set
of
of a set
of ![]() data points
data points
![]() to be a minimum is that
to be a minimum is that
![\begin{displaymath}
R^2(a,b) \equiv \sum_{i=1}^n [y_i-(a+bx_i)]^2
\end{displaymath}](l1_1062.gif)
![\begin{displaymath}
{\partial (R^2)\over\partial a} = -2\sum_{i=1}^n [y_i-(a+bx_i)] = 0
\end{displaymath}](l1_1063.gif)
![\begin{displaymath}
{\partial (R^2)\over\partial b} = -2\sum_{i=1}^n [y_i-(a+bx_i)]x_i = 0.
\end{displaymath}](l1_1064.gif)
![]() Matrix Inverse is
Matrix Inverse is
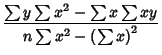
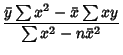
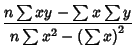
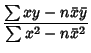
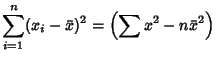
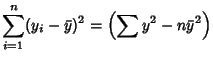
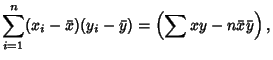
![]() is given by
is given by
![]() and
and ![]() are
are
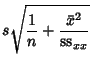
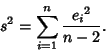
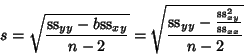
![]() th degree Polynomial
th degree Polynomial
![\begin{displaymath}
R^2 \equiv \sum_{i=1}^n [y_i-(a_0+a_1x_i+\ldots +a_k{x_i}^k)]^2.
\end{displaymath}](l1_1113.gif)
![$\left[{\matrix{n & \sum x& \cdots & \sum x^k\cr \sum x& \sum x^2& \cdots & \sum...
...right] = \left[{\matrix{\sum y\cr \sum xy\cr \vdots\cr \sum x^ky\cr}}\right]\!.$](l1_1120.gif)
![\begin{displaymath}
\left[{\matrix{1 & x_1 & \cdots & {x_1}^k\cr
1 & x_2 & \cdo...
...ght] = \left[{\matrix{y_1\cr y_2\cr \vdots\cr y_n\cr}}\right].
\end{displaymath}](l1_1121.gif)
![\begin{displaymath}
\left[{\matrix{1 & 1 & \cdots & 1\cr x_1 & x_2 & \cdots & x_...
...right] \left[{\matrix{y_1\cr y_2\cr \vdots\cr y_n\cr}}\right],
\end{displaymath}](l1_1122.gif)
![\begin{displaymath}
\left[{\matrix{n & \sum x& \cdots & \sum x^n\cr \sum x& \sum...
...{\matrix{\sum y\cr \sum xy\cr \vdots\cr \sum x^ky\cr}}\right].
\end{displaymath}](l1_1123.gif)
![\begin{displaymath}
\left[{\matrix{y_1\cr y_2\cr \vdots\cr y_m\cr}}\right] = \le...
...right] \left[{\matrix{a_0\cr a_1\cr \vdots\cr a_n\cr}}\right],
\end{displaymath}](l1_1125.gif)