The dot product can be defined by
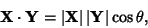 |
(1) |
where 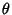 is the angle between the vectors. It follows immediately that
is the angle between the vectors. It follows immediately that
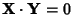 if
if 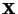 is Perpendicular to
is Perpendicular to 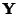 . The dot product is also called the Inner Product and written
. The dot product is also called the Inner Product and written
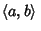 .
By writing
.
By writing
it follows that (1) yields
So, in general,
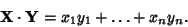 |
(5) |
The dot product is Commutative
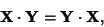 |
(6) |
Associative
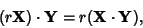 |
(7) |
and Distributive
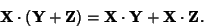 |
(8) |
The Derivative of a dot product of Vectors is
![\begin{displaymath}
{d\over dt} [{\bf r}_1(t)\cdot {\bf r}_2(t)]
= {\bf r}_1(t)...
...d{\bf r}_2\over dt} + {d{\bf r}_1\over dt} \cdot {\bf r}_2(t).
\end{displaymath}](d2_1499.gif) |
(9) |
The dot product is invariant under rotations
where Einstein Summation has been used.
The dot product is also defined for Tensors 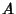 and
and 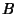 by
by
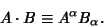 |
(11) |
See also Cross Product, Inner Product, Outer Product, Wedge Product
References
Arfken, G. ``Scalar or Dot Product.'' §1.3 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL:
Academic Press, pp. 13-18, 1985.
© 1996-9 Eric W. Weisstein
1999-05-24
![]() and
and ![]() by
by