|
|
|
For Vectors ![]() and
and ![]() ,
,
| (1) |
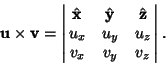 |
(2) |
| (3) | |||
| (4) |
| (5) |
Identities involving the cross product include
| (6) |
| (7) |
| (8) |
| (9) |
| (10) |
See also Dot Product, Scalar Triple Product
References
Arfken, G. ``Vector or Cross Product.'' §1.4 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL:
Academic Press, pp. 18-26, 1985.