Hyperbolic Geometry

A Non-Euclidean Geometry, also called Lobachevsky-Bolyai-Gauss Geometry, having constant Sectional Curvature $-1$. This Geometry satisfies all of Euclid's Postulates except the Parallel Postulate, which is modified to read: For any infinite straight Line $L$ and any Point $P$ not on it, there are many other infinitely extending straight Lines that pass through $P$ and which do not intersect $L$.

In hyperbolic geometry, the sum of Angles of a Triangle is less than 180°, and Triangles with the same angles have the same areas. Furthermore, not all Triangles have the same Angle sum (c.f. the AAA Theorem for Triangles in Euclidean 2-space). The best-known example of a hyperbolic space are Spheres in Lorentzian 4-space. The Poincaré Hyperbolic Disk is a hyperbolic 2-space. Hyperbolic geometry is well understood in 2-D, but not in 3-D.

Geometric models of hyperbolic geometry include the Klein-Beltrami Model, which consists of an Open Disk in the Euclidean plane whose open chords correspond to hyperbolic lines. A 2-D model is the Poincaré Hyperbolic Disk. Felix Klein constructed an analytic hyperbolic geometry in 1870 in which a Point is represented by a pair of Real Numbers $(x_1,x_2)$ with

$${x_1}^2+{x_2}^2<1$$

(i.e., points of an Open Disk in the Complex Plane) and the distance between two points is given by

$$d(x,X) = a\cosh^{-1}\!\!\left[{1-x_1X_1-x_2X_2\over \sqrt{1-{x_1}^2-{x_2}^2}\,\sqrt{1-{X_1}^2-{X_2}^2}}\right]\!\!.$$

The geometry generated by this formula satisfies all of Euclid's Postulates except the fifth. The Metric of this geometry is given by the Cayley-Klein-Hilbert Metric,

$$g_{11} = {a^2(1-{x_2}^2)\over (1-{x_1}^2-{x_2}^2)^2}$$

$$g_{12} = {a^2x_1x_2\over (1-{x_1}^2-{x_2}^2)^2}$$

$$g_{22} = {a^2(1-{x_1}^2)\over (1-{x_1}^2-{x_2}^2)^2}.$$

Hilbert extended the definition to general bounded sets in a Euclidean Space.

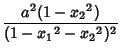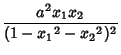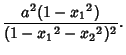See also Elliptic Geometry, Euclidean Geometry, Hyperbolic Metric, Klein-Beltrami Model, Non-Euclidean Geometry, Schwarz-Pick Lemma

References

Dunham, W. Journey Through Genius: The Great Theorems of Mathematics. New York: Wiley, pp. 57-60, 1990.

Eppstein, D. ``Hyperbolic Geometry.'' http://www.ics.uci.edu/~eppstein/junkyard/hyper.html.

Stillwell, J. Sources of Hyperbolic Geometry. Providence, RI: Amer. Math. Soc., 1996.