Complex Plane

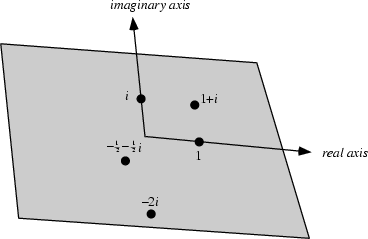
The plane of Complex Numbers spanned by the vectors 1 and $i$, where $i$ is the Imaginary Number. Every Complex Number corresponds to a unique Point in the complex plane. The Line in the plane with $i=0$ is the Real Line. The complex plane is sometimes called the Argand Plane or Gauss Plane, and a plot of Complex Numbers in the plane is sometimes called an Argand Diagram.

See also Affine Complex Plane, Argand Diagram, Argand Plane, Bergman Space, Complex Projective Plane

References

Courant, R. and Robbins, H. ``The Geometric Interpretation of Complex Numbers.'' §5.2 in What is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed. Oxford, England: Oxford University Press, pp. 92-97, 1996.