|
|
|
| (1) | |||
| (2) | |||
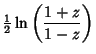 |
(3) | ||
| (4) | |||
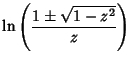 |
(5) | ||
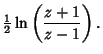 |
(6) |
References
Abramowitz, M. and Stegun, C. A. (Eds.). ``Hyperbolic Functions.'' §4.6 in
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, pp. 86-89, 1972.