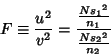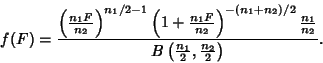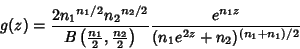Fisher's z-Distribution

$$g(z)={2{n_1}^{n_1/2}{n_2}^{n_2/2}\over B\left({{\textstyle{n... ...er 2}}}\right)} {e^{n_1z}\over (n_1e^{2z}+n_2)^{(n_1+n_1)/2}}$$ (1)

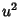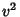(Kenney and Keeping 1951). This general distribution includes the Chi-Squared Distribution and Student's t-Distribution as special cases. Let $u^2$ and $v^2$ be Independent Unbiased Estimators of the Variance of a Normally Distributed variate. Define

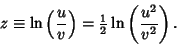$$z\equiv \ln\left({u\over v}\right)= {\textstyle{1\over 2}}\ln\left({u^2\over v^2}\right).$$ (2)

Then let

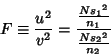$$F\equiv {u^2\over v^2} = {{N{s_1}^2\over n_1}\over {N{s_2}^2\over n_2}}$$ (3)

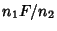so that $n_1F/n_2$ is a ratio of Chi-Squared variates

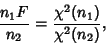$${n_1F\over n_2} = {\chi^2(n_1)\over \chi^2(n_2)},$$ (4)

which makes it a ratio of Gamma Distribution variates, which is itself a Beta Prime Distribution variate,

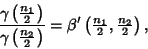$${\gamma\left({{\textstyle{n_1\over 2}}}\right)\over \gamma\l... ...t({{\textstyle{n_1\over 2}}, {\textstyle{n_2\over 2}}}\right),$$ (5)

giving

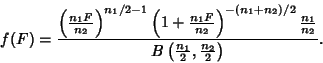$$f(F) = {\left({n_1F\over n_2}\right)^{n_1/2-1}\left({1+{n_1F... ...({{\textstyle{n_1\over 2}}, {\textstyle{n_2\over 2}}}\right)}.$$ (6)

The Mean is

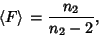$$\left\langle{F}\right\rangle{} = {n_2\over n_2-2},$$ (7)

and the Mode is

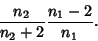$${n_2\over n_2+2} {n_1-2\over n_1}.$$ (8)

See also Beta Distribution, Beta Prime Distribution, Chi-Squared Distribution, Gamma Distribution, Normal Distribution, Student's t-Distribution

References

Kenney, J. F. and Keeping, E. S. Mathematics of Statistics, Pt. 2, 2nd ed. Princeton, NJ: Van Nostrand, pp. 180-181, 1951.