|
|
|
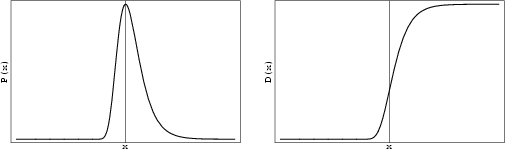
Also called the Extreme Value Distribution and Log-Weibull Distribution. It is the limiting distribution
for the smallest or largest values in a large sample drawn from a variety of distributions.
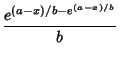 |
(1) | ||
| (2) |
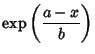 |
(3) | ||
| (4) | |||
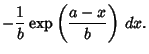 |
(5) |
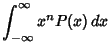 |
|||
![$\displaystyle {1\over b}\int_{-\infty}^\infty x^n\mathop{\rm exp}\nolimits \left({a\over x-b}\right)\mathop{\rm exp}\nolimits [-e^{(a-x)/b}]\,dx$](f_1370.gif) |
|||
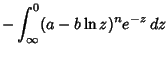 |
|||
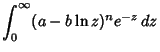 |
|||
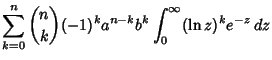 |
|||
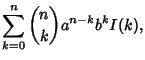 |
(6) |
| (7) | |||
| (8) | |||
| (9) | |||
| (10) | |||
| (11) |
| (12) | |||
| (13) | |||
![$\displaystyle {6\sqrt{6}\over b^3\pi^3}\{a^3+3a^2b\gamma+3ab^2(\gamma^2+{\textstyle{1\over 6}}\pi^2)+b^3[\gamma^3+{\textstyle{1\over 2}}\gamma\pi^2+2\zeta(3)]\}$](f_1389.gif) |
(14) | ||
| (15) |
| (16) |
See also Euler-Mascheroni Integrals, Gumbel's Distribution
|
|
|
© 1996-9 Eric W. Weisstein