|
|
|
N.B. A detailed on-line essay by S. Finch was the starting point for this entry.
Let ![]() denote the ``extreme'' (i.e., largest) Order Statistic
denote the ``extreme'' (i.e., largest) Order Statistic
![]() for a distribution of
for a distribution of ![]() elements
elements
![]() taken from a continuous Uniform Distribution. Then the distribution of the
taken from a continuous Uniform Distribution. Then the distribution of the ![]() is
is
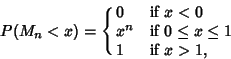 |
(1) |
| (2) | |||
| (3) |
If ![]() are taken from a Standard Normal Distribution, then its cumulative distribution is
are taken from a Standard Normal Distribution, then its cumulative distribution is
| (4) |
| (5) |
| (6) | |||
| (7) | |||
| (8) | |||
![$\displaystyle {3\over 2\sqrt{\pi}}\left[{1+{2\over\pi}\sin^{-1}({\textstyle{1\over 3}})}\right]$](e_2832.gif) |
(9) | ||
![$\displaystyle {5\over 4\sqrt{\pi}}\left[{1+{6\over\pi}\sin^{-1}({\textstyle{1\over 3}})}\right]$](e_2834.gif) |
(10) |
| (11) | |||
| (12) | |||
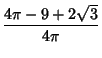 |
(13) | ||
![$\displaystyle 1+{\sqrt{3}\over\pi}-[\mu(4)]^2$](e_2841.gif) |
(14) | ||
![$\displaystyle 1+{5\sqrt{3}\over 4\pi}+{5\sqrt{3}\over 2\pi^2}\sin^{-1}({\textstyle{1\over 4}})-[\mu(5)]^2.$](e_2843.gif) |
(15) |
| (16) |
An analog to the Central Limit Theorem states that the asymptotic normalized distribution of ![]() satisfies one of the
three distributions
satisfies one of the
three distributions
| (17) | |||
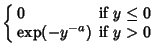 |
(18) | ||
![$\displaystyle \left\{\begin{array}{ll} \mathop{\rm exp}\nolimits [-(-y)^a] & \mbox{if $y\leq 0$}\\ 1 & \mbox{if $y>0$,}\end{array}\right.$](e_2850.gif) |
(19) |
See also Fisher-Tippett Distribution, Order Statistic
References
Balakrishnan, N. and Cohen, A. C. Order Statistics and Inference. New York: Academic Press, 1991.
David, H. A. Order Statistics, 2nd ed. New York: Wiley, 1981.
Finch, S. ``Favorite Mathematical Constants.'' http://www.mathsoft.com/asolve/constant/extval/extval.html
Gibbons, J. D. and Chakraborti, S. Nonparametric Statistical Inference, 3rd rev. ext. ed. New York: Dekker, 1992.
|
|
|
© 1996-9 Eric W. Weisstein