|
|
|
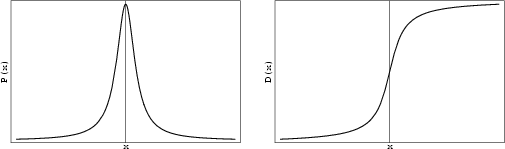
A Distribution published by William Gosset in 1908. His employer, Guinness Breweries, required him to publish under a
pseudonym, so he chose ``Student.'' Given ![]() independent measurements
independent measurements ![]() , let
, let
| (1) |
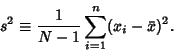 |
(2) |
Student's ![]() -distribution is arrived at by transforming to Student's z-Distribution with
-distribution is arrived at by transforming to Student's z-Distribution with
| (3) |
| (4) |
![$\displaystyle {\Gamma[{\textstyle{1\over 2}}(r+1)]\over\sqrt{r\pi}\,\Gamma({\textstyle{1\over 2}}r)\left({1+{t^2\over r}}\right)^{(r+1)/2}}$](s3_1254.gif) |
|||
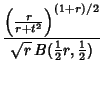 |
(5) | ||
![$\displaystyle \int_{-\infty}^t {\Gamma[{\textstyle{1\over 2}}(r+1)]\over \sqrt{...
...\,\Gamma({\textstyle{1\over 2}}r)\left({1+{t'^2\over r}}\right)^{(r+1)/2}}\,dt'$](s3_1257.gif) |
|||
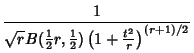 |
|||
![$\displaystyle {1\over 2}+{1\over 2}\left[{I(1; {\textstyle{1\over 2}}r, {\texts...
...{r\over r+t^2}, {\textstyle{1\over 2}}r, {\textstyle{1\over 2}}}\right)}\right]$](s3_1259.gif) |
|||
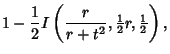 |
(6) |
| (7) |
| (8) |
The Mean, Variance, Skewness, and Kurtosis of Student's ![]() -distribution are
-distribution are
| (9) | |||
| (10) | |||
| (11) | |||
| (12) |
Beyer (1987, p. 514) gives 60%, 70%, 90%, 95%, 97.5%, 99%, 99.5%, and 99.95% confidence intervals, and
Goulden (1956) gives 50%, 90%, 95%, 98%, 99%, and 99.9% confidence intervals. A partial table is given
below for small ![]() and several common confidence intervals.
and several common confidence intervals.
| 80% | 90% | 95% | 99% | |
| 1 | 3.08 | 6.31 | 12.71 | 63.66 |
| 2 | 1.89 | 2.92 | 4.30 | 9.92 |
| 3 | 1.64 | 2.35 | 3.18 | 5.84 |
| 4 | 1.53 | 2.13 | 2.78 | 4.60 |
| 5 | 1.48 | 2.01 | 2.57 | 4.03 |
| 10 | 1.37 | 1.81 | 2.23 | 4.14 |
| 30 | 1.31 | 1.70 | 2.04 | 2.75 |
| 100 | 1.29 | 1.66 | 1.98 | 2.63 |
| 1.28 | 1.65 | 1.96 | 2.58 |
The so-called ![]() distribution is useful for testing if two observed distributions have the same Mean.
distribution is useful for testing if two observed distributions have the same Mean. ![]() gives the probability that the difference in two observed Means for a certain statistic
gives the probability that the difference in two observed Means for a certain statistic ![]() with
with ![]() Degrees of Freedom would be smaller than the observed value purely by chance:
Degrees of Freedom would be smaller than the observed value purely by chance:
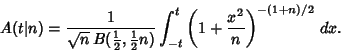 |
(13) |
| (14) |
The noncentral Student's ![]() -distribution is given by
-distribution is given by
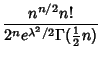 |
|||
![$\displaystyle \times \left\{{\sqrt{2}\,\lambda x(n+x^2)^{-(1+n/2)} {}_1F_1\left...
...a^2 x^2\over 2(n+x^2)}}\right)\over
\Gamma[{\textstyle{1\over 2}}(1+n)]}\right.$](s3_1280.gif) |
|||
![$\displaystyle \left.{+{e^{(\lambda^2 x^2)/[2(n+x^2)]}\sqrt{\pi}(n+x^2)^{-(n+1)/...
...x^2\over 2(n+x^2)}}\right)} \over \Gamma[{\textstyle{1\over 2}}(1+n)]}\right\},$](s3_1281.gif) |
(15) |
where ![]() is the Gamma Function,
is the Gamma Function,
![]() is a Confluent Hypergeometric Function,
and
is a Confluent Hypergeometric Function,
and ![]() is an associated Laguerre Polynomial.
is an associated Laguerre Polynomial.
See also Paired t-Test, Student's z-Distribution
References
Abramowitz, M. and Stegun, C. A. (Eds.).
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, pp. 948-949, 1972.
Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 536, 1987.
Fisher, R. A. ``Applications of `Student's' Distribution.'' Metron 5, 3-17, 1925.
Fisher, R. A. ``Expansion of `Student's' Integral in Powers of
Fisher, R. A. Statistical Methods for Research Workers, 10th ed. Edinburgh: Oliver and Boyd, 1948.
Goulden, C. H. Table A-3 in Methods of Statistical Analysis, 2nd ed. New York: Wiley, p. 443, 1956.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T.
``Incomplete Beta Function, Student's Distribution, F-Distribution, Cumulative Binomial Distribution.'' §6.2 in
Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge
University Press, pp. 219-223, 1992.
Spiegel, M. R. Theory and Problems of Probability and Statistics. New York: McGraw-Hill, pp. 116-117, 1992.
Student. ``The Probable Error of a Mean.'' Biometrika 6, 1-25, 1908.
![]() .'' Metron 5, 22-32, 1925.
.'' Metron 5, 22-32, 1925.
|
|
|
© 1996-9 Eric W. Weisstein