Area Principle

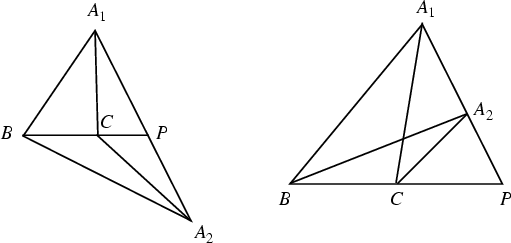
The ``Area principle'' states that

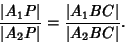$${\vert A_1P\vert\over\vert A_2P\vert}={\vert A_1BC\vert\over\vert A_2BC\vert}.$$ (1)

This can also be written in the form

$$\left[{A_1P\over A_2P}\right]=\left[{A_1BC\over A_2BC}\right],$$ (2)

where

$$\left[{AB\over CD}\right]$$ (3)

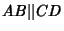is the ratio of the lengths $[A, B]$ and $[C, D]$ for $AB\vert\vert CD$ with a Plus or Minus Sign depending on if these segments have the same or opposite directions, and

$$\left[{ABC\over DEFG}\right]$$ (4)

is the Ratio of signed Areas of the Triangles. Grünbaum and Shepard show that Ceva's Theorem, Hoehn's Theorem, and Menelaus' Theorem are the consequences of this result.

See also Ceva's Theorem, Hoehn's Theorem, Menelaus' Theorem, Self-Transversality Theorem

References

Grünbaum, B. and Shepard, G. C. ``Ceva, Menelaus, and the Area Principle.'' Math. Mag. 68, 254-268, 1995.