|
|
|
A Polynomial invariant of a Knot discovered in 1923 by J. W. Alexander (Alexander 1928). In technical
language, the Alexander polynomial arises from the Homology of the infinitely cyclic cover
of a Knot's complement. Any generator of a Principal Alexander Ideal is called an
Alexander polynomial (Rolfsen 1976). Because the Alexander Invariant of a Tame Knot in ![]() has a
Square presentation Matrix, its Alexander Ideal is Principal and it has an Alexander polynomial denoted
has a
Square presentation Matrix, its Alexander Ideal is Principal and it has an Alexander polynomial denoted ![]() .
.
Let ![]() be the Matrix Product of Braid Words of a Knot, then
be the Matrix Product of Braid Words of a Knot, then
| (1) |
| (2) |
| (3) |
The Alexander polynomial remained the only known Knot Polynomial until the Jones Polynomial was
discovered in 1984. Unlike the Alexander polynomial, the more powerful Jones Polynomial does, in most cases,
distinguish Handedness. A normalized form of the Alexander polynomial symmetric in ![]() and
and ![]() and
satisfying
and
satisfying
| (4) |
| (5) |
| (6) | |||
| (7) | |||
| (8) |
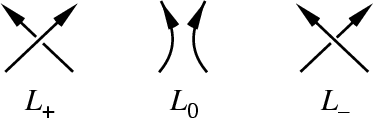
Let an Alexander polynomial be denoted ![]() , then there exists a Skein Relationship
(discovered by J. H. Conway)
, then there exists a Skein Relationship
(discovered by J. H. Conway)
| (9) |
| (10) |
For a Knot,
| (11) |
| (12) |
| (13) |
The HOMFLY Polynomial ![]() generalizes the Alexander polynomial (as well at the Jones Polynomial)
with
generalizes the Alexander polynomial (as well at the Jones Polynomial)
with
| (14) |
Rolfsen (1976) gives a tabulation of Alexander polynomials for Knots up to 10 Crossings and Links up to 9 Crossings.
See also Braid Group, Jones Polynomial, Knot, Knot Determinant, Link, Skein Relationship
References
Adams, C. C. The Knot Book: An Elementary Introduction to the Mathematical Theory of Knots. New York:
W. H. Freeman, pp. 165-169, 1994.
Alexander, J. W. ``Topological Invariants of Knots and Links.'' Trans. Amer. Math. Soc. 30, 275-306, 1928.
Alexander, J. W. ``A Lemma on a System of Knotted Curves." Proc. Nat. Acad. Sci. USA 9, 93-95, 1923.
Doll, H. and Hoste, J. ``A Tabulation of Oriented Links.'' Math. Comput. 57, 747-761, 1991.
Jones, V. ``A Polynomial Invariant for Knots via von Neumann Algebras.'' Bull. Amer. Math. Soc. 12, 103-111, 1985.
Rolfsen, D. ``Table of Knots and Links.'' Appendix C in Knots and Links. Wilmington, DE:
Publish or Perish Press, pp. 280-287, 1976.
Stoimenow, A. ``Alexander Polynomials.'' http://www.informatik.hu-berlin.de/~stoimeno/ptab/a10.html.
Stoimenow, A. ``Conway Polynomials.'' http://www.informatik.hu-berlin.de/~stoimeno/ptab/c10.html.
|
|
|
© 1996-9 Eric W. Weisstein