Given a Seifert Form 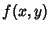 , choose a basis
, choose a basis 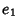 , ...,
, ..., 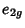 for
for 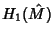 as a Z-module so every
element is uniquely expressible as
as a Z-module so every
element is uniquely expressible as
with 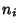 integer, define the Seifert matrix
integer, define the Seifert matrix 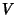 as the
as the 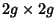 integral Matrix with entries
integral Matrix with entries
The right-hand Trefoil Knot has Seifert matrix
A Seifert matrix is not a knot invariant, but it can be used to distinguish between different
Seifert Surfaces for a given knot.
See also Alexander Matrix
References
Rolfsen, D. Knots and Links. Wilmington, DE: Publish or Perish Press, pp. 200-203, 1976.
© 1996-9 Eric W. Weisstein
1999-05-26
![]() , choose a basis
, choose a basis ![]() , ...,
, ..., ![]() for
for ![]() as a Z-module so every
element is uniquely expressible as
as a Z-module so every
element is uniquely expressible as