|
|
|
Also called Artin Braid Groups. Consider ![]() strings, each oriented vertically from a lower to an
upper ``bar.'' If this is the least number of strings needed to make a closed braid representation of a Link,
strings, each oriented vertically from a lower to an
upper ``bar.'' If this is the least number of strings needed to make a closed braid representation of a Link, ![]() is
called the Braid Index. Now enumerate the possible braids in a group, denoted
is
called the Braid Index. Now enumerate the possible braids in a group, denoted ![]() . A general
. A general ![]() -braid is
constructed by iteratively applying the
-braid is
constructed by iteratively applying the ![]() (
(
![]() ) operator, which switches the lower endpoints of the
) operator, which switches the lower endpoints of the ![]() th
and
th
and ![]() th strings--keeping the upper endpoints fixed--with the
th strings--keeping the upper endpoints fixed--with the ![]() th string brought above the
th string brought above the ![]() th string.
If the
th string.
If the ![]() th string passes below the
th string passes below the ![]() th string, it is denoted
th string, it is denoted ![]() .
.
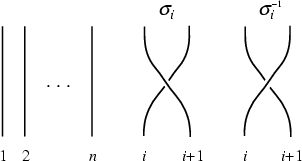
Topological equivalence for different representations of a Braid Word
![]() and
and
![]() is guaranteed by the conditions
is guaranteed by the conditions
References
Birman, J. S. ``Braids, Links, and the Mapping Class Groups.'' Ann. Math. Studies, No. 82. Princeton, NJ:
Princeton University Press, 1976.
Birman, J. S. ``Recent Developments in Braid and Link Theory.'' Math. Intell. 13, 52-60, 1991.
Jones, V. F. R. ``Hecke Algebra Representations of Braid Groups and Link Polynomials.'' Ann. Math. 126, 335-388, 1987.
![]() Christy, J. ``Braids.''
http://www.mathsource.com/cgi-bin/MathSource/Applications/Mathematics/0202-228.
Christy, J. ``Braids.''
http://www.mathsource.com/cgi-bin/MathSource/Applications/Mathematics/0202-228.
![]() Weisstein, E. W. ``Knots and Links.'' Mathematica notebook Knots.m.
Weisstein, E. W. ``Knots and Links.'' Mathematica notebook Knots.m.