An Ideal 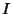 of a Ring
of a Ring 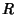 is called principal if there is an element
is called principal if there is an element 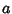 of
of 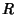 such that
such that
In other words, the Ideal is generated by the element 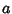 . For example, the Ideals
. For example, the Ideals 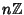 of
the Ring of Integers
of
the Ring of Integers 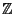 are all principal, and in fact
all Ideals of
are all principal, and in fact
all Ideals of 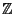 are principal.
are principal.
See also Ideal, Ring
© 1996-9 Eric W. Weisstein
1999-05-26
![]() of a Ring
of a Ring ![]() is called principal if there is an element
is called principal if there is an element ![]() of
of ![]() such that
such that