Triangle Squaring

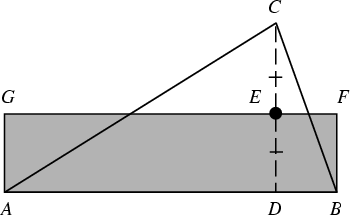
$\begin{figure}\begin{center}\BoxedEPSF{TriangleSquaring.epsf}\end{center}\end{figure}$

Let be the Altitude of a Triangle $\Delta ABC$ and let be its Midpoint. Then

$\begin{displaymath} \mathop{\rm area}(\Delta ABC)={\textstyle{1\over 2}}AB\cdot CD = AB\cdot DE, \end{displaymath}$

and $\vbox{\hrule height.6pt\hbox{\vrule width.6pt height6pt \kern10.6pt \vrule width.6pt} \hrule height.6pt}ABFG$ can be squared by Rectangle Squaring. The general Polygon can be treated by drawing diagonals, squaring the constituent triangles, and then combining the squares together using the Pythagorean Theorem.

See also Pythagorean Theorem, Rectangle Squaring

References

Dunham, W. ``Hippocrates' Quadrature of the Lune.'' Ch. 1 in Journey Through Genius: The Great Theorems of Mathematics. New York: Wiley, pp. 14-15, 1990.