Newton's Diverging Parabolas

Curves with Cartesian equation

$$ay^2 = x(x^2 - 2bx +c)$$

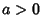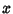with $a > 0$. The above equation represents the third class of Newton's classification of Cubic Curves, which Newton divided into five species depending on the Roots of the cubic in $x$ on the right-hand side of the equation. Newton described these cases as having the following characteristics:

1. ``All the Roots are Real and unequal. Then the Figure is a diverging Parabola of the Form of a Bell, with an Oval at its Vertex.

2. Two of the Roots are equal. A Parabola will be formed, either Nodated by touching an Oval, or Punctate, by having the Oval infinitely small.

3. The three Roots are equal. This is the Neilian Parabola, commonly called Semi-cubical.

4. Only one Real Root. If two of the Roots are impossible, there will be a Pure Parabola of a Bell-like Form''

(MacTutor Archive).

References

MacTutor History of Mathematics Archive. ``Newton's Diverging Parabolas.'' http://www-groups.dcs.st-and.ac.uk/~history/Curves/Newtons.html.