|
|
|
The Newton-Cotes formulas are an extremely useful and straightforward family of Numerical Integration techniques.
To integrate a function ![]() over some interval
over some interval ![]() , divide it into
, divide it into ![]() equal parts such that
equal parts such that ![]() and
and
![]() . Then find Polynomials which approximate the tabulated function, and integrate them to
approximate the Area under the curve. To find the fitting Polynomials, use Lagrange
Interpolating Polynomials. The resulting formulas are called Newton-Cotes formulas, or
Quadrature Formulas.
. Then find Polynomials which approximate the tabulated function, and integrate them to
approximate the Area under the curve. To find the fitting Polynomials, use Lagrange
Interpolating Polynomials. The resulting formulas are called Newton-Cotes formulas, or
Quadrature Formulas.
Newton-Cotes formulas may be ``closed'' if the interval ![]() is included in the fit, ``open'' if the points
is included in the fit, ``open'' if the points
![]() are used, or a variation of these two. If the formula uses
are used, or a variation of these two. If the formula uses ![]() points (closed or open), the
Coefficients of terms sum to
points (closed or open), the
Coefficients of terms sum to ![]() .
.
If the function ![]() is given explicitly instead of simply being tabulated at the values
is given explicitly instead of simply being tabulated at the values ![]() , the best numerical
method of integration is called Gaussian Quadrature. By picking the intervals at which to sample the function,
this procedure produces more accurate approximations (but is significantly more complicated to implement).
, the best numerical
method of integration is called Gaussian Quadrature. By picking the intervals at which to sample the function,
this procedure produces more accurate approximations (but is significantly more complicated to implement).
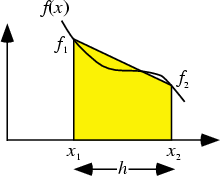
The 2-point closed Newton-Cotes formula is called the Trapezoidal Rule because it approximates the area under a
curve by a Trapezoid with horizontal base and sloped top (connecting the endpoints ![]() and
and ![]() ). If the first
point is
). If the first
point is ![]() , then the other endpoint will be located at
, then the other endpoint will be located at
| (1) |
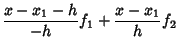 |
|||
| (2) |
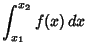 |
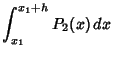 |
||
| (3) |
The 3-point rule is known as Simpson's Rule. The Abscissas are
| (4) | |||
| (5) |
|
|
|
|
|
|
|
|
|
|
|
(6) |
| (7) |
The 4-point closed rule is Simpson's 3/8 Rule,
| (8) |
| (9) |
| (10) |
|
|
|
|
|
(11) |
|
|
|
|
|
|
|
|
(12) |
|
|
|
|
|
(13) |
|
|
|
|
|
|
|
|
(14) |
|
|
|
|
|
|
|
|
|
|
|
(15) |
Closed ``extended'' rules use multiple copies of lower order closed rules to build up higher order rules. By
appropriately tailoring this process, rules with particularly nice properties can be constructed. For ![]() tabulated points, using
the Trapezoidal Rule
tabulated points, using
the Trapezoidal Rule ![]() times and adding the results gives
times and adding the results gives
|
|
|
|
|
|
|
|
|
|
|
(16) |
|
|
|
|
|
|
|
|
(17) |
|
|
|
|
|
|
|
|
|
|
|
(18) |
| (19) |
|
|
|
|
|
|
|
|
|
|
|
(20) |
|
|
|
|
|
(21) |
| (22) |
|
|
|
|
|
(23) |
| (24) |
Other Newton-Cotes rules occasionally encountered include Durand's Rule
| (25) |
|
|
|
|
|
(26) |
| (27) |
The open Newton-Cotes rules use points outside the integration interval, yielding the
1-point
| (28) |
|
|
|
|
|
|
|
|
(29) |
| (30) |
| (31) |
| (32) |
|
|
|
|
|
(33) |
|
|
|
|
|
(34) |
A 2-point open extended formula is
|
|
|
|
|
|
|
|
(35) |
Single interval extrapolative rules estimate the integral in an interval based on the points around it. An
example of such a rule is
| (36) |
| (37) |
| (38) |
| (39) |
See also Bode's Rule, Difference Equation, Durand's Rule, Finite Difference, Gaussian Quadrature, Hardy's Rule, Lagrange Interpolating Polynomial, Numerical Integration, Simpson's Rule, Simpson's 3/8 Rule, Trapezoidal Rule, Weddle's Rule
References
Abramowitz, M. and Stegun, C. A. (Eds.). ``Integration.'' §25.4 in
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, pp. 885-887, 1972.
Beyer, W. H. (Ed.) CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 127, 1987.
Hildebrand, F. B. Introduction to Numerical Analysis. New York: McGraw-Hill, pp. 160-161, 1956.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. ``Classical Formulas for Equally Spaced Abscissas.'' §4.1 in
Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England:
Cambridge University Press, pp. 124-130, 1992.
|
|
|
© 1996-9 Eric W. Weisstein