|
|
|
N.B. A detailed on-line essay by S. Finch was the starting point for this entry.
Let ![]() be a compact connected subset of
be a compact connected subset of ![]() -dimensional Euclidean Space. Gross (1964) and Stadje (1981) proved
that there is a unique Real Number
-dimensional Euclidean Space. Gross (1964) and Stadje (1981) proved
that there is a unique Real Number ![]() such that for all
such that for all ![]() ,
, ![]() , ...,
, ..., ![]() , there exists
, there exists ![]() with
with
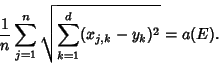 |
(1) |
| (2) |
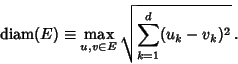 |
(3) |
| (4) |
| (5) |
| (6) |
| (7) |
|
|
|
|
|
|
![${d\over d+1}\leq M(d)\leq {[\Gamma({\textstyle{1\over 2}}d)]^2 2^{d-2}\sqrt{2d}\over \Gamma(d-{\textstyle{1\over 2}})\sqrt{(d+1)\pi}} < \sqrt{d\over d+1}$](m_238.gif) |
where ![]() is the Gamma Function (Nikolas and Yost 1988).
is the Gamma Function (Nikolas and Yost 1988).
An unrelated quantity characteristic of a given Magic Square is also known as a Magic Constant.
References
Finch, S. ``Favorite Mathematical Constants.'' http://www.mathsoft.com/asolve/constant/magic/magic.html
Cleary, J.; Morris, S. A.; and Yost, D. ``Numerical Geometry--Numbers for Shapes.'' Amer. Math. Monthly 95, 260-275, 1986.
Croft, H. T.; Falconer, K. J.; and Guy, R. K. Unsolved Problems in Geometry. New York: Springer-Verlag, 1994.
Gross, O. The Rendezvous Value of Metric Space. Princeton, NJ: Princeton University Press, pp. 49-53, 1964.
Nikolas, P. and Yost, D. ``The Average Distance Property for Subsets of Euclidean Space.'' Arch. Math. (Basel) 50, 380-384, 1988.
Stadje, W. ``A Property of Compact Connected Spaces.'' Arch. Math. (Basel) 36, 275-280, 1981.
|
|
|
© 1996-9 Eric W. Weisstein